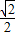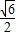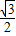题目内容
已知双曲线的焦点在x轴上,离心率为2,F1、F2为左、右焦点.P为双曲线上一点,且∠F1PF2=60°,
=123,求双曲线的标准方程.
解:如图,设双曲线方程为
=1(a＞0,b＞0).
因为e=
=2,所以c=2a.
由双曲线的定义||PF1|-|PF2||=2a=c,
在△PF1F2中,由余弦定理,得
|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos60°=(|PF1|-|PF2|)2+2|PF1||PF2|(1-cos60°),即4c2=c2+|PF1||PF2|.①
又
=12
,所以
|PF1||PF2|sin60°=12
,即|PF1||PF2|=48.②
由①②,得c2=16,c=4,则a=2,b2=c2-a2=12.所以所求的双曲线方程为
=1.
练习册系列答案
相关题目
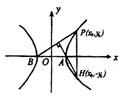已知双曲线的焦点在x轴上，且过点A（1，0）和B（-1，0），P是双曲线上异于A、B的任一点，如果△APB的垂心H总在双曲线上，求双曲线的标准方程．
的右焦点作x轴的垂线交椭圆于A、B两点,已知双曲线的焦点在x轴上,对称中心在坐标原点且两条渐近线分别过A、B两点,则双曲线的离心率e为( )
B.
C.
D.
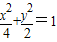的右焦点作x轴的垂线交椭圆于A、B两点，已知双曲线的焦点在x轴上，对称中心在坐标原点且两条渐近线分别过A、B两点，则双曲线的离心率是（ ）
