题目内容
18．已知
.
（Ⅰ）当
时，求数列
的前n项和
；
（Ⅱ）求
.
18. （Ⅰ）解：当a=b时，un=(n＋1)an，这时数列{un}的前n项和
Sn=2a+3a2+4a3+…+nan+1+(n+1)an ①
①式两边同乘以a，得
aSn=2a2+3a3+4a4+…+nan+(n+1)an+1 ②
①式减去②式，得
（1－a）Sn=2a+a2+a3+…+an－(n+1)an+1.
若a≠1, （1－a）Sn=－(n+1)an+1+a
Sn=
=
若a=1, Sn=2+3+…+n+(n+1)
=.
（Ⅱ）解：由（Ⅰ），当a=b时，un=(n+1)an,则
=
=
=a
当a≠b时，un=an+an－1b+…+abn－1+bn
= an [1+
+(
)2+…+(
)n]
=an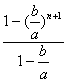
=
（an+1－bn+1）.
此时，
若a>b>0,
=
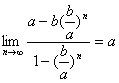
若b>a>0,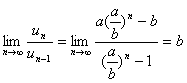
练习册系列答案
阶梯计算系列答案
相关题目
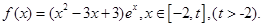
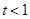时，求函数
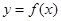的单调区间;
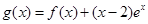，试问函数
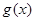在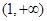
上是否存在保值区间？若存在，请求出一个保值区间；若不存在，请说明理由.
时，求
的单调递增区间；
且
时，
求
的值
时，求曲线
在点
处的切线方程；
时，若
在区间
上的最小值为-2，求
的取值范围；
，且
恒成立，求
时，求函数
的单调区间；
上是减函数，求实数a的取值范围.
时，求函数
的最大值；
时，设点
、
是函数
的图象上任意不同的两点，求证：直线
的斜率
.