题目内容
4．讨论关于x的方程（x-1）（3-x）=a-x（1＜x＜3）在a∈R时解的个数．分析 由题意，判断x2-5x+a+3=0在（1，3）上个实根的个数，即a=-x2+5x-3，x∈（1，3）实根的个数，利用图象，即可得出结论．
解答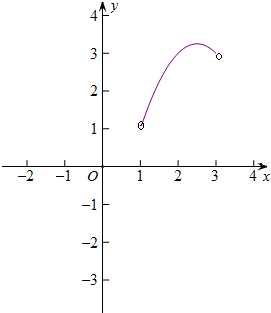 
解：由题意，判断x2-5x+a+3=0在（1，3）上个实根的个数．
即a=-x2+5x-3，x∈（1，3）实根的个数，
令f（x）=-x2+5x-3，x∈（1，3），
f（1）=1，f（3）=3，f（$\frac{5}{2}$）=$\frac{13}{4}$，
当1＜a≤3或a=$\frac{13}{4}$时，方程有1个实根，
当3＜a＜$\frac{13}{4}$时，方程有2个实根，
当a≤1或a＞$\frac{13}{4}$时，方程有无实根．
点评 本题考查二次方程实根分布问题，考查等价转化思想，属于中档题．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
在
单调递减，则
的取值范围是（ ）
B．
D．
13．若函数f（x）=x+$\frac{b}{x}$（b∈R）的导函数在区间（2，4）上有零点，则f（x）在下列区间单调递增的是（ ）
| A． | （2，+∞） | B． | （-∞，-3） | C． | （$\sqrt{2}$，2） | D． | （-8，-4） |