题目内容
已知函数![]() (
(![]() ,
,![]() ),
),![]() .
.
(Ⅰ)证明:当![]() 时,对于任意不相等的两个正实数
时,对于任意不相等的两个正实数![]() 、
、![]() ,均有
,均有![]() 成立;
成立;
(Ⅱ)记![]() ,
,
(ⅰ)若![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(ⅱ)证明:![]() .
.
(Ⅰ)证明:![]() ,
,
![]() ,
,
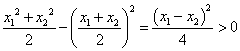 ,则
,则![]() ①
①
![]() ,则
,则![]() ,②
,②
由①②知![]() .………………………………
.………………………………![]() 分
分
(Ⅱ)(ⅰ)![]() ,
,
![]() ,
,
令![]() ,则
,则![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,则当
,则当![]() 时,
时,![]() 恒成立,
恒成立,
即当![]() 时,
时,![]() 恒成立. …………………………… 5分
恒成立. …………………………… 5分
令![]() ,则当
,则当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 上单调递减,从而
上单调递减,从而![]() ,
,
故![]() .……………………………………………………7分
.……………………………………………………7分
(ⅱ)法一:
![]() ,
,
令![]() ,
,
则![]() 表示
表示![]() 上一点
上一点![]() 与直线
与直线![]() 上一点
上一点![]() 距离的平方.… 8分
距离的平方.… 8分
令![]() ,则
,则![]() ,
,
可得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
故![]() ,则
,则![]() ,…………………………………… 10分
,…………………………………… 10分
直线![]() 与
与![]() 的图象相切与点
的图象相切与点![]() ,
,
点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
则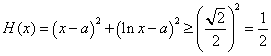 ,
,
故![]() .……………………………………………………12分
.……………………………………………………12分
法二:
![]() ,
,
令![]() ,则
,则![]() .………………8分
.………………8分
令![]() ,则
,则![]() ,显然
,显然![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,………………………………………………………………………………10分
上单调递增,………………………………………………………………………………10分
则![]() ,则
,则![]() ,故
,故![]() .…………………12分
.…………………12分

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|