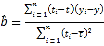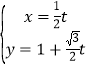题目内容
【题目】已知椭圆![]() ,
,![]() 为左、右焦点,直线
为左、右焦点,直线![]() 过
过![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点.
两点.
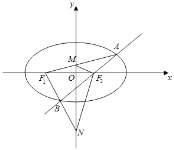
(1)若![]() 垂直于
垂直于![]() 轴时,求
轴时,求![]() ;
;
(2)当![]() 时,
时,![]() 在
在![]() 轴上方时,求
轴上方时,求![]() ,
,![]() 的坐标;
的坐标;
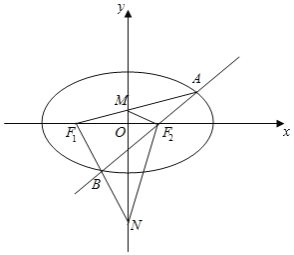
(3)若直线![]() 交
交![]() 轴于
轴于![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,是否存在直线
,是否存在直线![]() ,使
,使![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() ,
,![]() (3)存在直线
(3)存在直线![]() 或
或![]()
【解析】
(1)由椭圆方程可求得右焦点坐标,进一步求得![]() ,
,![]() 的坐标,即可求出
的坐标,即可求出![]() ;
;
(2)设![]() ,由
,由![]() ,利用数量积为0可得
,利用数量积为0可得![]() 与
与![]() 的方程,再由
的方程,再由![]() 在椭圆上,得
在椭圆上,得![]() 与
与![]() 的另一方程,联立即可求得
的另一方程,联立即可求得![]() 的坐标,从而得到直线
的坐标,从而得到直线![]() 的方程,与椭圆方程联立即可求得
的方程,与椭圆方程联立即可求得![]() 的坐标;
的坐标;
(3)设![]() ,
,![]() ,直线
,直线![]() :
:![]() (斜率为零时不满足题意),联立直线方程与椭圆方程,结合
(斜率为零时不满足题意),联立直线方程与椭圆方程,结合![]() ,得
,得![]() ,再由直线
,再由直线![]() 的方程:
的方程:![]() ,得
,得![]() 纵坐标
纵坐标![]() ,由直线
,由直线![]() 的方程:
的方程:![]() ,得N的纵坐标
,得N的纵坐标![]() ,结合根与系数的关系,得
,结合根与系数的关系,得![]() ,解得
,解得![]() 值,从而得到直线方程.
值,从而得到直线方程.
(1)依题意,![]() ,当
,当![]() 轴时,则
轴时,则![]() ,
,![]() ,得
,得![]() ;
;
(2)设![]() ,∵
,∵![]() ,
,
∴![]() ,
,
又![]() 在椭圆上,满足
在椭圆上,满足![]() ,即
,即![]() ,
,
∴![]() ,解得
,解得![]() ,即
,即![]() .
.
直线![]() ,
,
联立 ,解得
,解得![]() ;
;
(3)设![]() ,
,![]() ,
,
直线![]() :
:![]() (斜率为零时不满足题意),
(斜率为零时不满足题意),
则![]() ,
,![]() .
.
联立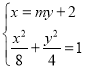 ,得
,得![]() .
.
则![]() ,
,![]() .
.
由直线![]() 的方程:
的方程:![]() ,得
,得![]() 纵坐标
纵坐标![]() ;
;
由直线![]() 的方程:
的方程:![]() ,得
,得![]() 的纵坐标
的纵坐标![]() .
.
若![]() ,即
,即![]() ,
,
 ,
,
![]() ,即
,即![]() ,
,
∴![]() ,解得
,解得![]() .
.
∴存在直线![]() 或
或![]() 满足题意.
满足题意.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某大学生参加社会实践活动,对某公司1月份至6月份销售某种配件的销售量及销售单价进行了调查,销售单价![]() 和销售量
和销售量![]() 之间的一组数据如下表所示:
之间的一组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14.2 |
(1)根据1至5月份的数据,先求出![]() 关于
关于![]() 的回归直线方程;6月份的数据作为检验数据.若由回归直线方程得到的预测数据与检验数据的误差不超过
的回归直线方程;6月份的数据作为检验数据.若由回归直线方程得到的预测数据与检验数据的误差不超过![]() ,则认为所得到的回归直线方程是理想的.试问所求得的回归直线方程是否理想?
,则认为所得到的回归直线方程是理想的.试问所求得的回归直线方程是否理想?
(2)预计在今后的销售中,销售量与销售单价仍然服从(1)中的回归关系,如果该种机器配件的成本是![]() 元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考数据:![]() ,
,![]() .
.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: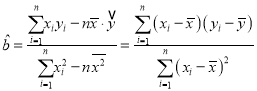 ,
,![]() .
.