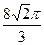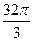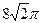题目内容
设地球的半径为R,在北纬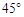 圈上有两个点A、B,A在西经
圈上有两个点A、B,A在西经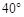 ,B在东经
,B在东经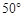 ,则A、B两点间的球面距离为( )
,则A、B两点间的球面距离为( )
A.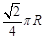 B.
B.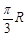 C.
C.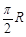 D.
D.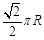
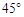 圈上有两个点A、B,A在西经
圈上有两个点A、B,A在西经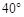 ,B在东经
,B在东经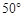 ,则A、B两点间的球面距离为( )
,则A、B两点间的球面距离为( )A.
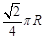 B.
B.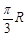 C.
C.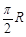 D.
D.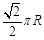
B
如图所示:
地心为O,O1为北纬45°圈的圆心;
则∠AO1B=360°-130°-140°=90°,∠O1AO=45°。

∴O1A=
 R。
R。∴AB=
 O1A=R。
O1A=R。∴OA=OB=AB。
∴∠AOB=
 。
。∴A、B两点的球面距离为
 ·R=
·R= ,故选B。
,故选B。
练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
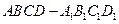 中,E,F分别是
中,E,F分别是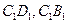 的中点,G为
的中点,G为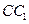 上任一点,EC与底面ABCD所成角的正切值是4.
上任一点,EC与底面ABCD所成角的正切值是4. 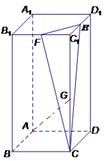
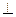 EF;
EF;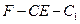 的余弦值。
的余弦值。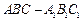 中,侧面
中,侧面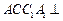
 平面
平面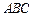 ,
,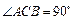 .
.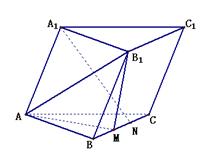
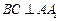 ;
;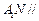 平面
平面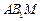 .
.
 +2
+2 +6,8
+6,8
 是边长为
是边长为 的正三角形,俯视图为正六边形,那么该几何体的侧视图的面积为
的正三角形,俯视图为正六边形,那么该几何体的侧视图的面积为




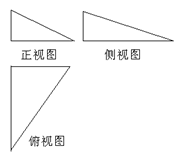
 的平面去截该球,所得截面面积为
的平面去截该球,所得截面面积为 ,则该球的体积( )
,则该球的体积( )