题目内容
【题目】已知圆![]() :
:![]() ,圆
,圆![]() :
:![]() .
.
(Ⅰ)设直线![]() 被圆
被圆![]() 所截得的弦的中点为
所截得的弦的中点为![]() ,判断点
,判断点![]() 与圆
与圆![]() 的位置关系;
的位置关系;
(Ⅱ)设圆![]() 被圆
被圆![]() 截得的一段圆弧(在圆
截得的一段圆弧(在圆![]() 内部,含端点)为
内部,含端点)为![]() ,若直线
,若直线![]() :
:![]() 与圆弧
与圆弧![]() 只有一个公共点,求实数
只有一个公共点,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)点![]() 在圆
在圆![]() 上.(Ⅱ)
上.(Ⅱ)![]() 或
或![]() .
.
【解析】
(Ⅰ)将直线方程代入圆的方程,消去![]() ,得到
,得到![]() ,则
,则![]() ,从而得到
,从而得到![]() 的横坐标为2,再代入直线方程求出
的横坐标为2,再代入直线方程求出![]() 的坐标,即可判断点与圆
的坐标,即可判断点与圆![]() 的位置关系;
的位置关系;
(2)设![]() 和
和![]() 的交点为
的交点为![]() ,
,![]() ,直线
,直线![]() 恒过的定点为
恒过的定点为![]() ,求出两圆的交点坐标,
,求出两圆的交点坐标,
分直线![]() 与圆
与圆![]() 相切时,与直线
相切时,与直线![]() 与圆弧
与圆弧![]() 相交两种情况计算可得.
相交两种情况计算可得.
解:(1)将![]() 代入圆
代入圆![]() 的方程可得
的方程可得![]() .
.
设此方程的两实根分别为![]() ,
,![]() ,则
,则![]() .
.
所以点![]() 的横坐标为2,从而可得
的横坐标为2,从而可得![]() .
.
因为![]() ,所以点
,所以点![]() 在圆
在圆![]() 上.
上.
(Ⅱ)如图,因为直线![]() :
:![]() ,
,![]() 解得
解得![]() ,即直线恒过的定点为
,即直线恒过的定点为![]() .
.
设![]() 和
和![]() 的交点为
的交点为![]() ,
,![]() ,直线
,直线![]() 恒过的定点为
恒过的定点为![]() .
.
由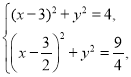 解得
解得![]() ,
,![]() .
.
所以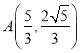 ,
,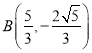 .
.
(ⅰ)当直线![]() 与圆
与圆![]() 相切时.
相切时.
由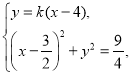 可得
可得![]() .
.
令![]() ,则
,则![]() .
.
此时解得![]() ,切点在圆弧
,切点在圆弧![]() 上,符合题意.
上,符合题意.
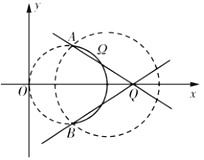
(ⅱ)当直线![]() 与圆弧
与圆弧![]() 相交时,由图可知,要使交点只有一个,则
相交时,由图可知,要使交点只有一个,则![]() 在
在![]() 和
和![]() 之间.
之间.
因为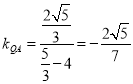 ,
,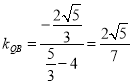 ,
,
所以![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目