题目内容
用数学归纳法证明对于n≥0的整数An=11n+2+122n+1能被133整除.
证明:(1)当n=0时,A0=112+12=133能被133整除.
(2)假设n=k时,A k =11k+2+122k+1能被133整除.
当n=k+1时,
Ak+1=11k+3+122k+3=11·11k+2+122·122k+1
=11·11k+2+11·122k+1+(122-11)·122k+1
=11·(11k+2+122k+1)+133·122k+1.
∴n=k+1时,命题也成立.
根据(1)(2),知对于任意整数n≥0,命题都成立.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
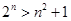 对于
对于 的自然数
的自然数 都成立”时,第一步证明中的起始值
都成立”时,第一步证明中的起始值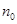 应取( )
应取( ) ”对于
”对于 的正整数
的正整数 均成立”时,第一步证明中的起始值
均成立”时,第一步证明中的起始值 应取( )
应取( ) 对于
对于 的自然数
的自然数 都成立”时,第一步证明中的起始值
都成立”时,第一步证明中的起始值 应取_____________.
应取_____________. 对于
对于 的正整数
的正整数 均成立”时,第一步证明中的起始值
均成立”时,第一步证明中的起始值 应取( )
应取( )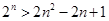 对于
对于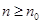 的正整数
的正整数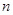 均成立”时,第一步证明中的起始值
均成立”时,第一步证明中的起始值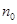 应取( )
应取( )