题目内容
已知lg2=a,lg3=b,则lg215=
;(试用a,b表示)
| 1+b-a |
| a |
| 1+b-a |
| a |
分析:运用对数的运算性质,把log215化为lg2,lg3和常数的形式,然后代入lg2=a,lg3=b即可.
解答:解:∵lg2=a,lg3=b,
∴log215=log23+log25=log23+log2
=
+log210-1=
+
-1
=
+
-1=
.
故答案为
.
∴log215=log23+log25=log23+log2
| 10 |
| 2 |
=
| lg3 |
| lg2 |
| lg3 |
| lg2 |
| 1 |
| lg2 |
=
| b |
| a |
| 1 |
| a |
| 1+b-a |
| a |
故答案为
| 1+b-a |
| a |
点评:本题考查对数式的换底公式的应用,对数的运算性质,是基础题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
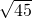 的值为 ________.
的值为 ________. 的值为 .
的值为 .