题目内容
选修4-1:几何证明选讲.
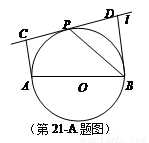
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证:
(1) ![]() ;
;
(2) AB2=BE![]() BD-AE
BD-AE![]() AC.
AC.
 |
【命题意图】本小题主要平面几何的证明,具体涉及到四点共圆、相交弦定理及三角形相似等内容.
【试题解析】证明:⑴连结AD,因为AB为圆的直径,所以∠ADB=90°, (2分)
又EF⊥AB,∠EFA=90°,则A、D、E、F四点共圆,
∴∠DEA=∠DFA. (5分)
⑵由(1)知,BD![]() BE=BA
BE=BA![]() BF.
BF.
又△ABC∽△AEF,∴![]() ,即AB
,即AB![]() AF=AE
AF=AE![]() AC. (7分)
AC. (7分)
∴ BE![]() BD-AE
BD-AE![]() AC =BA
AC =BA![]() BF-AB
BF-AB![]() AF =AB(BF-AF) =AB2. (10分)
AF =AB(BF-AF) =AB2. (10分)
 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
A.选修4-1:几何证明选讲
|
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD.求证:(1)l是⊙O的切线;(2)PB平分∠ABD.
B.选修4-2:矩阵与变换
(本小题满分10分)
已知点A在变换:T:→=作用后,再绕原点逆时针旋转90°,得到点B.若点B坐标为(-3,4),求点A的坐标.
C.选修4-4:坐标系与参数方程
(本小题满分10分)
求曲线C1:被直线l:y=x-所截得的线段长.
D.选修4-5:不等式选讲
(本小题满分10分)
已知a、b、c是正实数,求证:≥.
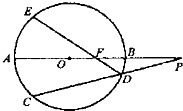 (2013•太原一模)选修4一1:几何证明选讲
(2013•太原一模)选修4一1:几何证明选讲
 选修4一1:几何证明选讲
选修4一1:几何证明选讲 为半圆
为半圆 的直径,
的直径, ,
, 为半圆上一点,过点
为半圆上一点,过点 ,过点
,过点 作
作 于
于 ,交半圆于点
,交半圆于点 ,
, .
.
 平分
平分 ;
; 的长.
的长. ABC中的两条角平分线
ABC中的两条角平分线 和
和 相交于
相交于 ,
, B=60
B=60 ,
, 在
在 上,且
上,且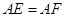 。
。  四点共圆;
四点共圆;