题目内容
已知函数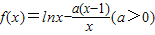 .
.(1)求f(x)的最小值;
(2)证明:不等式
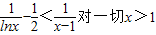 恒成立.
恒成立.
【答案】分析:(1)求导函数,确定函数的单调性,从而可求f(x)的最小值;
(2)只需证明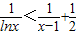 ,即证
,即证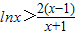 ,构造g(x)=
,构造g(x)=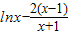 ,确定其单调性,可得结论.
,确定其单调性,可得结论.
解答:(1)解:∵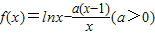 ,∴
,∴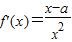
∴f(x)在(0,a)上递减,在(a,+∞)上递增
∴f(x)的最小值为f(a)=lna+1-a;
(2)证明:只需证明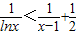 ,即证
,即证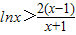
令g(x)=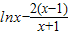 ,则g′(x)=
,则g′(x)=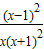 >0
>0
∵x>1,∴g′(x)>0,∴g(x)在(1,+∞)上单调递增,
∴g(x)>g(1)=0,∴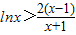
故原不等式成立.
点评:本题考查导数知识的运用,考查函数的单调性,考查不等式的证明,确定函数的单调性是关键.
(2)只需证明
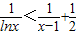 ,即证
,即证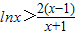 ,构造g(x)=
,构造g(x)=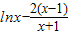 ,确定其单调性,可得结论.
,确定其单调性,可得结论.解答:(1)解:∵
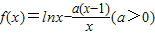 ,∴
,∴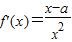
∴f(x)在(0,a)上递减,在(a,+∞)上递增
∴f(x)的最小值为f(a)=lna+1-a;
(2)证明:只需证明
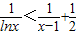 ,即证
,即证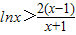
令g(x)=
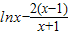 ,则g′(x)=
,则g′(x)=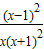 >0
>0∵x>1,∴g′(x)>0,∴g(x)在(1,+∞)上单调递增,
∴g(x)>g(1)=0,∴
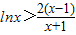
故原不等式成立.
点评:本题考查导数知识的运用,考查函数的单调性,考查不等式的证明,确定函数的单调性是关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.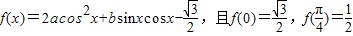 .
. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.