题目内容
17.如图各网格是单位正方形,粗线所表示的图形为某几何体的三视图.则该几何体的体积为( )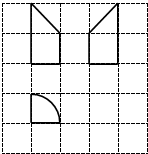
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
分析 根据几何体的三视图,得出该几何体是$\frac{1}{4}$圆柱体和椎体的组合体,结合图中数据求出它的体积.
解答 解:根据几何体的三视图,得;
该几何体是$\frac{1}{4}$圆柱体和锥体的组合体,
且它们的底面都是半径为1的$\frac{1}{4}$圆面,高都为1;
所以该几何体的体积为
$\frac{1}{4}$•π•12•1+$\frac{1}{3}$•$\frac{1}{4}$•π•12•1=$\frac{π}{3}$.
故选:B.
点评 本题考查了几何体三视图的应用问题,解题的关键是根据三视图得出几何体的结构特征,是基础题目.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
7.设f(x)=x2+11x+7.则f(x+1)=( )
| A. | x2-13x+19 | B. | x2-13x+18 | C. | x2+13x+19 | D. | x2+13x+18 |
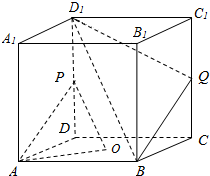 如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P、Q分别是棱DD1、CC1的中点.
如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P、Q分别是棱DD1、CC1的中点.