题目内容
已知向量 ,且
,且 ,求:
,求:
(1) 及
及 ;
;
(2)若 的最小值为
的最小值为 ,求实数
,求实数 的值.
的值.
(1)详见解析;(2)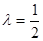 .
.
解析试题分析:(1)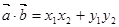 ,
,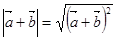 ,代入数值求解;
,代入数值求解;
(2)根据前一问的结果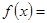
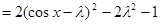 ,根据
,根据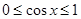 ,讨论当
,讨论当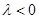 ,
,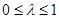 ,
,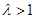 三种情况的最小值,解得
三种情况的最小值,解得 的值.
的值.
试题解析:解:(1)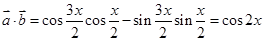 (2分)
(2分)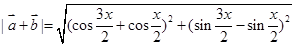
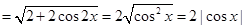 (5分)
(5分)
又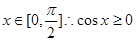 从而
从而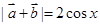 (6分)
(6分)
(2)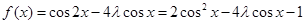
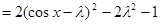 (7分)
(7分)
由于 故
故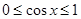 (8分)
(8分)
①当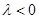 时,当且仅当
时,当且仅当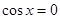 时,
时,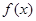 取得最小值
取得最小值 ,这与题设矛盾 (9分)
,这与题设矛盾 (9分)
②当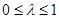 时,当且仅当
时,当且仅当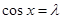 时,
时,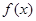 取得最小值
取得最小值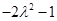 ,由
,由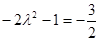 及
及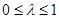 得
得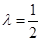 (11分)
(11分)
③当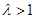 时,当且仅当
时,当且仅当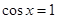 时,
时,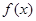 取得最小值
取得最小值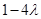 ,由
,由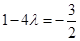 ,
,
得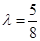 与
与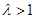 矛盾 (13分)
矛盾 (13分)
综上所述,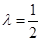 即为所求. (14分)
即为所求. (14分)
考点:1.向量的计算公式;2.分类讨论二次函数求最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. 的最小正周期;
的最小正周期; ,且
,且 ,求
,求 .
.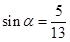 ,且
,且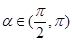 .
.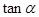 的值; (2)求
的值; (2)求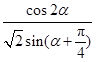 的值.
的值. 
 的最小正周期;
的最小正周期; ,求
,求 的值域.
的值域.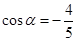 ,
,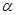 为第三象限角.
为第三象限角.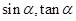 的值;(2)求
的值;(2)求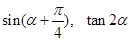 的值.
的值. .
. 的值;
的值; 的值.
的值. 
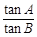 =
=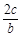 .
.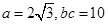 ,求
,求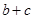 的值。
的值。 sin2
sin2 +cos
+cos