题目内容
点P(a,b)是双曲线x2-y2=1右支上一点,且P到渐近线距离为
,则a+b=
或2
或2.
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:依题意,可得到关于a,b的方程组,解之即可.
解答:解:∵点P(a,b)是双曲线x2-y2=1右支上一点,
∴a2-b2=1且a>0,①
又P到渐近线y=±x距离为
,
∴
=
②或
=
③,
若
=
∴a-b=±2;
当a-b=2时,代入①得:a+b=
;
当a-b=-2时,代入①得:a+b=-
,此时a=-
,与a>0矛盾,故舍去;
若
=
③,
∴a+b=±2.
当a+b=2时,a-b=
可解得a=
,符合题意;
同理可得,当a+b=-2时,a-b=-
,解得a=-
(舍去);
综上所述,a+b=2或a+b=
.
∴a2-b2=1且a>0,①
又P到渐近线y=±x距离为
| 2 |
∴
| |a-b| | ||
|
| 2 |
| |a+b| | ||
|
| 2 |
若
| |a-b| | ||
|
| 2 |
∴a-b=±2;
当a-b=2时,代入①得:a+b=
| 1 |
| 2 |
当a-b=-2时,代入①得:a+b=-
| 1 |
| 2 |
| 5 |
| 4 |
若
| |a+b| | ||
|
| 2 |
∴a+b=±2.
当a+b=2时,a-b=
| 1 |
| 2 |
| 5 |
| 4 |
同理可得,当a+b=-2时,a-b=-
| 1 |
| 2 |
| 5 |
| 4 |
综上所述,a+b=2或a+b=
| 1 |
| 2 |
点评:本题考查双曲线的简单性质,考查方程思想与分类讨论思想,考查运算能力,属于难题.

练习册系列答案
相关题目
 为坐标原点,
为坐标原点, ,
,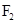 是双曲线
是双曲线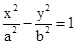 (a>0,b>0)的焦点,若在双曲
(a>0,b>0)的焦点,若在双曲 ,则该双曲线的渐近线方程为(
)
,则该双曲线的渐近线方程为(
) y=0
B.
y=0
B. =0 D.
=0 D. ±y=0
±y=0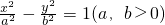 的虚轴长为2
的虚轴长为2 ,渐近线方程是y=
,渐近线方程是y=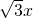 ,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且
,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且 .
. 的虚轴长为2
的虚轴长为2 ,渐近线方程是y=
,渐近线方程是y= ,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且
,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且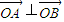 .
.