题目内容
给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点.
(1)设l的斜率为1,求![]() 与
与![]() 的夹角的大小;
的夹角的大小;
(2)设![]() =λ
=λ![]() ,若λ∈[4,9],求l在y轴上截距的变化范围.
,若λ∈[4,9],求l在y轴上截距的变化范围.
答案:
解析:
解析:
|
解:(1)C的焦点为F(1,0),直线l的斜率为1,所以l的方程为y=x-1. 将y=x-1代入方程y2=4x,并整理得x2-6x+1=0. 设A(x1,y1),B(x2,y2),则有x1+x2=6,x1x2=1. | cos( 所以 (2)由题设 得(x2-1,y2)=λ(1-x1,-y1), 即 由②得y22=λ2y12,∵y12=4x1,y22=4x2, ∴x2=λ2x1.③联立①、③解得x2=λ,依题意有λ>0. ∴B(λ,2 (λ-1)y=2 当λ∈[4,9]时,l在方程y轴上的截距为 由 ∴ 直线l在y轴上截距的变化范围为[- 分析:本小题主要考查抛物线的性质,直线与抛物线的关系以及解析几何的基本方法、思想和综合解题能力. |

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
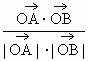 =-
=-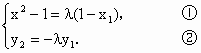
 =2
=2 ,求直线l的方程.
,求直线l的方程.  与C相交于A、B两点。
与C相交于A、B两点。 与
与 夹角的余弦值;
夹角的余弦值; ,若
,若 ∈[4,9],求
∈[4,9],求