题目内容
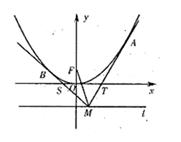
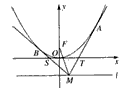
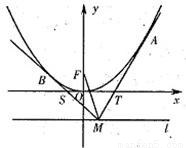
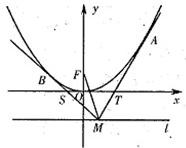 如图,以原点O为顶点,以y轴为对称轴的抛物线E的焦点为F(0,1),点M是直线l:y=m(m<0)上任意一点,过点M引抛物线E的两条切线分别交x轴于点S,T,切点分别为B,A.
如图,以原点O为顶点,以y轴为对称轴的抛物线E的焦点为F(0,1),点M是直线l:y=m(m<0)上任意一点,过点M引抛物线E的两条切线分别交x轴于点S,T,切点分别为B,A.(I)求抛物线E的方程;
(Ⅱ)求证:点S,T在以FM为直径的圆上;
(Ⅲ)当点M在直线l上移动时,直线AB恒过焦点F,求m的值.
分析:(1)设抛物线方程为x2=2py,根据焦点坐标可得到
=1,进而得到p的值,从而确定抛物线的方程.
(2)设点A(x1,y1),B(x2,y2),然后对抛物线方程进行求导,表示出切线AM的斜率进而得到切线方程,然后令y=0可求出T的坐标进而得到直线FT的斜率,根据kAM•kFT=-1可验证点T在以FM为直径的圆上;同理可证点S在以FM为直径的圆上.
(3)根据抛物线的焦点坐标,设斜率为k可得到直线AB的方程,然后与抛物线方程联立消去y,得到关于x的一元二次方程,进而可得到两根之积等于-4,设点M(x0,m),切线AM、BM的方程过点M可得到可消去x0,再由x1x2=-4可得m的值.
| p |
| 2 |
(2)设点A(x1,y1),B(x2,y2),然后对抛物线方程进行求导,表示出切线AM的斜率进而得到切线方程,然后令y=0可求出T的坐标进而得到直线FT的斜率,根据kAM•kFT=-1可验证点T在以FM为直径的圆上;同理可证点S在以FM为直径的圆上.
(3)根据抛物线的焦点坐标,设斜率为k可得到直线AB的方程,然后与抛物线方程联立消去y,得到关于x的一元二次方程,进而可得到两根之积等于-4,设点M(x0,m),切线AM、BM的方程过点M可得到可消去x0,再由x1x2=-4可得m的值.
解答: 解:(I)设抛物线E的方程为x2=2py(p>0),
解:(I)设抛物线E的方程为x2=2py(p>0),
依题意
=1,解得p=2,
所以抛物线E的方程为x2=4y.
(Ⅱ)设点A(x1,y1),B(x2,y2).x1x2≠0,否则切线不过点M
∵y=
x2,y′=
x,∴切线AM的斜率kAM=
x1,
方程为y-y1=
x1(x-x1),其中y1=
.
令y=0,得x=
x1,点T的坐标为(
x1,0),
∴直线FT的斜率kFT=-
,
∵kAM•kFT=
x1•(-
)=-1,
∴AM⊥FT,即点T在以FM为直径的圆上;
同理可证点S在以FM为直径的圆上,
所以S,T在以FM为直径的圆上.
(Ⅲ)抛物线x2=4y焦点F(0,1),可设直线AB:y=kx+1.
由
得x2-4kx-4=0,
则x1x2=-4.
由(Ⅱ)切线AM的方程为y=
x1x-
过点M(x0,m),
得m=
x1x0-
,
同理m=
x2x0-
.
消去x0,得m(x1-x2)=
x1x2(x1-x2)
∵x1≠x2,由上x1x2=-4
∴m=
x1x2=-1,即m的值为-1.
 解:(I)设抛物线E的方程为x2=2py(p>0),
解:(I)设抛物线E的方程为x2=2py(p>0),依题意
| p |
| 2 |
所以抛物线E的方程为x2=4y.
(Ⅱ)设点A(x1,y1),B(x2,y2).x1x2≠0,否则切线不过点M
∵y=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
方程为y-y1=
| 1 |
| 2 |
| ||
| 4 |
令y=0,得x=
| 1 |
| 2 |
| 1 |
| 2 |
∴直线FT的斜率kFT=-
| 2 |
| x1 |
∵kAM•kFT=
| 1 |
| 2 |
| 2 |
| x1 |
∴AM⊥FT,即点T在以FM为直径的圆上;
同理可证点S在以FM为直径的圆上,
所以S,T在以FM为直径的圆上.
(Ⅲ)抛物线x2=4y焦点F(0,1),可设直线AB:y=kx+1.
由
|
则x1x2=-4.
由(Ⅱ)切线AM的方程为y=
| 1 |
| 2 |
| 1 |
| 4 |
| x | 2 1 |
得m=
| 1 |
| 2 |
| 1 |
| 4 |
| x | 2 1 |
同理m=
| 1 |
| 2 |
| 1 |
| 4 |
| x | 2 2 |
消去x0,得m(x1-x2)=
| 1 |
| 4 |
∵x1≠x2,由上x1x2=-4
∴m=
| 1 |
| 4 |
点评:本题主要考查抛物线的标准方程、直线与抛物线的联立问题.圆锥曲线经常作为压轴题出现,基础知识一定要熟练掌握才能做正确.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
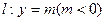 上任意一点,过点M引抛物线E的两条切线分别交x轴于点S , T,切点分别为B、A。
上任意一点,过点M引抛物线E的两条切线分别交x轴于点S , T,切点分别为B、A。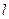 上移动时,直线AB恒过焦点F,求
上移动时,直线AB恒过焦点F,求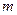 的值。
的值。