题目内容
【题目】如图所示，射线OA、OB分别与x轴正半轴成45°和30°角，过点P(1,0)作直线AB分别交OA、OB于A、B两点，当AB的中点C恰好落在直线y＝
x上时，求直线AB的方程．
【答案】(3＋
)x－2y－3－
＝0.
【解析】解：由题意可得kOA＝tan45°＝1，
kOB＝tan(180°－30°)＝－
，
所以射线OA的方程为y＝x(x≥0)，
射线OB的方程为y＝－
x(x≥0)．
设A(m，m)，B(－
n，n)，
所以AB的中点C(
， 
)，
由点C在y＝
x上，且A、P、B三点共线得
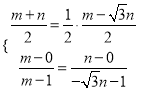
解得m＝
，
所以A(
， 
)．
又P(1,0)，
所以kAB＝kAP＝
＝
，
所以直线AB的方程为y＝
(x－1)，
即直线AB的方程为(3＋
)x－2y－3－
＝0.
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
