题目内容
点P是△ABC内一点且满足4
+3
+2
=
，则△PBC，△PAC，△PAB的面积比为（ ）
| PA |
| PB |
| PC |
| 0 |
| A、4：3：2 |
| B、2：3：4 |
| C、1：1：1 |
| D、3：4：6 |
分析：如图所示，过点C作CD∥PA交BP的延长线于点D，AC与PD交于点E．由于4
+3
+2
=
，可得2
+
+
=
．得到
=2
，
=
．利用相似三角形的性质可得
=
=
，同理
=
．即可得出．
| PA |
| PB |
| PC |
| 0 |
| PA |
| 3 |
| 2 |
| PB |
| PC |
| 0 |
| CD |
| PA |
| PD |
| 3 |
| 2 |
| AP |
| S△PAB |
| S△PBC |
|
| ||
|
|
| 1 |
| 2 |
| S△PAB |
| S△PAC |
| 2 |
| 3 |
解答：解：如图所示，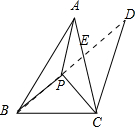
过点C作CD∥PA交BP的延长线于点D，AC与PD交于点E．
∵4
+3
+2
=
，∴2
+
+
=
．
∴
=2
，
=
．
∴
=
=
，同理
=
．
∴S△PBC：S△PAC：S△PAB=4：3：2．
故选：A．
过点C作CD∥PA交BP的延长线于点D，AC与PD交于点E．
∵4
| PA |
| PB |
| PC |
| 0 |
| PA |
| 3 |
| 2 |
| PB |
| PC |
| 0 |
∴
| CD |
| PA |
| PD |
| 3 |
| 2 |
| BP |
∴
| S△PAB |
| S△PBC |
|
| ||
|
|
| 1 |
| 2 |
| S△PAB |
| S△PAC |
| 2 |
| 3 |
∴S△PBC：S△PAC：S△PAB=4：3：2．
故选：A．
点评：本题考查了向量的三角形法则、共线定理、相似三角形的性质，属于难题．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
点P是△ABC内一点，且
=
+
，则△ABP的面积与△ABC的面积之比是（ ）
| AP |
| 2 |
| 5 |
| AB |
| 1 |
| 5 |
| AC |
| A、1：5 | B、2：5 |
| C、1：2 | D、2：1 |