题目内容
某足球俱乐部2013年10月份安排4次体能测试,规定:按顺序测试,一旦测试合格就不必参加以后的测试,否则4次测试都要参加。若运动员小李4次测试每次合格的概率组成一个公差为 的等差数列,他第一次测试合格的概率不超过
的等差数列,他第一次测试合格的概率不超过 ,且他直到第二次测试才合格的概率为
,且他直到第二次测试才合格的概率为 。
。
(Ⅰ)求小李第一次参加测试就合格的概率P1;
(2)求小李10月份参加测试的次数x的分布列和数学期望。
 的等差数列,他第一次测试合格的概率不超过
的等差数列,他第一次测试合格的概率不超过 ,且他直到第二次测试才合格的概率为
,且他直到第二次测试才合格的概率为 。
。(Ⅰ)求小李第一次参加测试就合格的概率P1;
(2)求小李10月份参加测试的次数x的分布列和数学期望。
(Ⅰ)小李第一次参加测试就合格的概率为 ;(Ⅱ)则x的分布列为
;(Ⅱ)则x的分布列为
小李10月份参加测试的次数x的数学期望为 .
.
 ;(Ⅱ)则x的分布列为
;(Ⅱ)则x的分布列为| x | 1 | 2 | 3 | 4 |
| P |  |  |  |  |
 .
. 试题分析:(Ⅰ)求小李第一次参加测试就合格的概率,由题意小李4次测试每次合格的概率组成一个公差为
 的等差数列,可设第一次参加测试就合格的概率为
的等差数列,可设第一次参加测试就合格的概率为 ,则小李四次测试合格的概率依次为
,则小李四次测试合格的概率依次为 ,而他直到第二次测试才合格的概率为
,而他直到第二次测试才合格的概率为 ,即
,即 ,解得
,解得 或
或 ,又因为他第一次测试合格的概率不超过
,又因为他第一次测试合格的概率不超过 ,可舍去
,可舍去 ;(Ⅱ)求小李10月份参加测试的次数x的分布列和数学期望,小李10月份参加测试的次数为
;(Ⅱ)求小李10月份参加测试的次数x的分布列和数学期望,小李10月份参加测试的次数为 ,则
,则 ,小李四次考核每次合格的概率依次为
,小李四次考核每次合格的概率依次为 ,根据相互独立事件同时发生的概率,得到分布列和期望.
,根据相互独立事件同时发生的概率,得到分布列和期望.试题解析:(Ⅰ)设小李四次测试合格的概率依次为:
a, a+
 , a+
, a+ , a+
, a+ (a≤
(a≤ ), (2分)
), (2分)则(1-a)(a+
 )=
)= ,即
,即 ,
,解得
 (舍), (5分)
(舍), (5分)所以小李第一次参加测试就合格的概率为
 ; (6分)
; (6分)(Ⅱ)因为P(x=1)=
 , P(x=2)=
, P(x=2)= ,P(x=3)=
,P(x=3)= ,
,P(x=4)=1-P(x=1)-P(x=2)-P(x=3)=
 , (8分)
, (8分)则x的分布列为
| x | 1 | 2 | 3 | 4 |
| P |  |  |  |  |
所以
 ,
, 即小李10月份参加测试的次数x的数学期望为
 . (12分)
. (12分)
练习册系列答案
相关题目
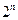 ,则算过关。问:(Ⅰ)某人在这项游戏中最多能过几关?(Ⅱ)他连过前三关的概率是多少?(注:骰子是一个在各面上分别有1,2,3,4,5,6点数的均匀正方体。抛掷骰子落地静止后,向上一面的点数为出现点数。)
,则算过关。问:(Ⅰ)某人在这项游戏中最多能过几关?(Ⅱ)他连过前三关的概率是多少?(注:骰子是一个在各面上分别有1,2,3,4,5,6点数的均匀正方体。抛掷骰子落地静止后,向上一面的点数为出现点数。)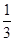 .
.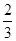 ,乙获胜的概率是
,乙获胜的概率是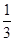 ,则比赛以甲三胜一负而结束的概率为________.
,则比赛以甲三胜一负而结束的概率为________.



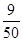 ;
; ,第二、第三种产品受欢迎的概率分别为
,第二、第三种产品受欢迎的概率分别为 ,
, ,且不同种产品是否受欢迎相互独立.记
,且不同种产品是否受欢迎相互独立.记 为公司向市场投放三种新型产品受欢迎的数量,其分布列为
为公司向市场投放三种新型产品受欢迎的数量,其分布列为

 .
.