题目内容
(2011•东城区一模)已知椭圆C的中心在坐标原点,焦点在x轴上,离心率为
,椭圆C上的点到焦点距离的最大值为3.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若过点P(0,m)的直线l与椭圆C交于不同的两点A,B,且
=3
,求实数m的取值范围.
| 1 |
| 2 |
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若过点P(0,m)的直线l与椭圆C交于不同的两点A,B,且
| AP |
| PB |
分析:(Ⅰ)由题设条件知
⇒
,由此能求出椭圆方程.
(Ⅱ)若过点P(0,m)的斜率不存在,则m=±
.若过点P(0,m)的直线斜率为k,即:m≠±
时,直线AB的方程为y-m=kx.由
⇒(3+4k2)x2+8kmx+4m2-12=0,△=64m2k2-4(3+4k2)(4m2-12).因为AB和椭圆C交于不同两点,所以△>0.由此能求出实数m的取值范围.
|
|
(Ⅱ)若过点P(0,m)的斜率不存在,则m=±
| ||
| 2 |
| ||
| 2 |
|
解答:解:(Ⅰ)设所求的椭圆方程为:
+
=1 (a>b>0)
由题意:
⇒
所求椭圆方程为:
+
=1.…(5分)
(Ⅱ)若过点P(0,m)的斜率不存在,则m=±
.
若过点P(0,m)的直线斜率为k,
即:m≠±
时,
直线AB的方程为y-m=kx
由
⇒(3+4k2)x2+8kmx+4m2-12=0,
△=64m2k2-4(3+4k2)(4m2-12),
因为AB和椭圆C交于不同两点,
所以△>0,4k2-m2+3>0,
所以4k2>m2-3 ①
设A(x1,y1),B(x2,y2),
由已知
=3
,
则x1+x2=-
,x1x2=
②
=(-x1,m-y1),
=(x2,y2-m)-x1=3x2 ③
将③代入②得:-3(
)2=
整理得:16m2k2-12k2+3m2-9=0
所以k2=
代入①式,
得4k2=
>m2-3
<0,
解得
<m2<3.
所以-
<m<-
或
<m<
.
综上可得,实数m的取值范围为:(-
,-
]∪[
,
).…(14分)
| x2 |
| a2 |
| y2 |
| b2 |
由题意:
|
|
所求椭圆方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)若过点P(0,m)的斜率不存在,则m=±
| ||
| 2 |
若过点P(0,m)的直线斜率为k,
即:m≠±
| ||
| 2 |
直线AB的方程为y-m=kx
由
|
△=64m2k2-4(3+4k2)(4m2-12),
因为AB和椭圆C交于不同两点,
所以△>0,4k2-m2+3>0,
所以4k2>m2-3 ①
设A(x1,y1),B(x2,y2),
由已知
| AP |
| PB |
则x1+x2=-
| 8km |
| 3+4k2 |
| 4m2-12 |
| 3+4k2 |
| AP |
| PB |
将③代入②得:-3(
| 4km |
| 3+4k2 |
| 4m2-12 |
| 3+4k2 |
整理得:16m2k2-12k2+3m2-9=0
所以k2=
| 9-3m2 |
| 16m2-12 |
得4k2=
| 9-3m2 |
| 4m2-3 |
| 4m2(m2-3) |
| 4m2-3 |
解得
| 3 |
| 4 |
所以-
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
综上可得,实数m的取值范围为:(-
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
点评:通过几何量的转化考查用待定系数法求曲线方程的能力,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.

练习册系列答案
相关题目
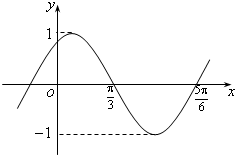 (2011•东城区一模)已知函数y=sin(ωx+φ)
(2011•东城区一模)已知函数y=sin(ωx+φ)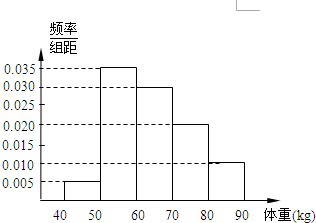 (2011•东城区一模)从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).由图中数据可知体重的平均值为
(2011•东城区一模)从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).由图中数据可知体重的平均值为