题目内容
已知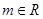 ,函数
,函数
(1)求 的极小值;
的极小值;
(2)若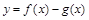 在
在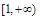 上为单调增函数,求
上为单调增函数,求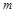 的取值范围;
的取值范围;
(3)设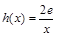 ,若在
,若在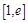 (
(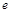 是自然对数的底数)上至少存在一个
是自然对数的底数)上至少存在一个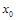 ,使得
,使得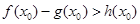 成立,求
成立,求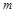 的取值范围.
的取值范围.
【答案】
1)由题意, ,
, ,∴当
,∴当 时,
时, ;当
;当 时,
时, ,所以,
,所以, 在
在 上是减函数,在
上是减函数,在 上是增函数,故
上是增函数,故 .
.
(2)  ,
, ,由于
,由于 在
在 内为单调增函数,所以
内为单调增函数,所以 在
在 上恒成立,即
上恒成立,即 在
在 上恒成立,故
上恒成立,故 ,所以
,所以 的取值范围是
的取值范围是 .…………………9分
.…………………9分
(3)构造函数 ,
,
当 时,由
时,由 得,
得, ,
, ,所以在
,所以在 上不存在一个
上不存在一个 ,使得
,使得 .
.
当 时,
时, ,因为
,因为 ,所以
,所以 ,
, ,所以
,所以 在
在 上恒成立,故
上恒成立,故 在
在 上单调递增,
上单调递增, ,所以要在
,所以要在 上存在一个
上存在一个 ,使得
,使得 ,必须且只需
,必须且只需 ,解得
,解得 ,故
,故 的取值范围是
的取值范围是 .…………………14分
.…………………14分
另法:(Ⅲ)当 时,
时, .
.
当 时,由
时,由 ,得
,得  , 令
, 令 ,则
,则 ,所以
,所以 在
在 上递减,
上递减, .
.
综上,要在 上存在一个
上存在一个 ,使得
,使得 ,必须且只需
,必须且只需 .
.
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
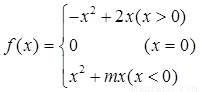
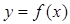 的图象;
的图象;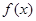 在区间[-1,
在区间[-1,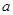 -2]上单调递增,试确定
-2]上单调递增,试确定
 ,函数
,函数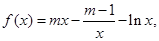
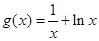 .
. 的极值;
的极值; 在
在 上为单调递增函数,求
上为单调递增函数,求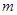 的取值范围;
的取值范围;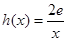 ,若在
,若在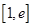 (
( 是自然对数的底数)上至少存在一个
是自然对数的底数)上至少存在一个 ,使得
,使得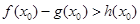 成立,求
成立,求 .
.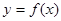 的图象;
的图象;
 ,函数
,函数
 的最小正周期;
的最小正周期; 时,求函数
时,求函数