题目内容
在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且EF=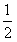 BC。
BC。
(Ⅰ)证明:FO∥平面CDE;
(Ⅱ)设BC=2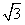 ,CD=2,OE=
,CD=2,OE=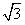 ,求EC与平面ABCD所成角的正弦值。
,求EC与平面ABCD所成角的正弦值。
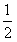 BC。
BC。(Ⅰ)证明:FO∥平面CDE;
(Ⅱ)设BC=2
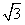 ,CD=2,OE=
,CD=2,OE=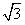 ,求EC与平面ABCD所成角的正弦值。
,求EC与平面ABCD所成角的正弦值。 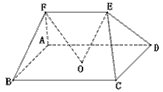
| (Ⅰ)证明:取CD的中点M,连结OM, 在矩形ABCD中,  , ,又  ,则 ,则 , ,连结EM,于是四边形EFOM为平行四边形, ∴FO∥EM, 又  平面CDE,且EM 平面CDE,且EM 平面CDE, 平面CDE, ∴FO∥平面CDE。 (Ⅱ)连结FM,由(Ⅰ)和已知条件,在等边△CDE中,CM=DM, EM⊥CD,且  , ,又  , ,因此,平行四边形EFOM为菱形, 过E作EG⊥OM于G, ∵CD⊥EM,CD⊥OM, ∴CD⊥平面EOM,∴CD⊥EG, 因此,EG⊥平面ABCD,所以,∠EGC为EC与底面ABCD所成角, 在△EOM中,  ,则△EOM为正三角形, ,则△EOM为正三角形,∴点E到平面ABCD的距离为  , ,所以,  , ,即EC与平面CDF所成角的正弦值为  。 。 |
 |

练习册系列答案
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
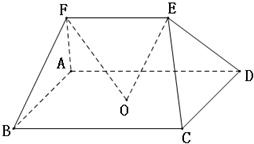 在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且
在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且 在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,平面CDE是等边三角形,棱EF∥BC且EF=
在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,平面CDE是等边三角形,棱EF∥BC且EF=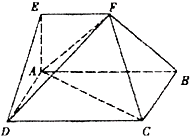 如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=2,AD=AE=EF=1,平面ABFE⊥平面ABCD.
如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=2,AD=AE=EF=1,平面ABFE⊥平面ABCD.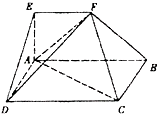 如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF,∠EAB=90°,平面ABFE⊥平面ABCD.
如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF,∠EAB=90°,平面ABFE⊥平面ABCD.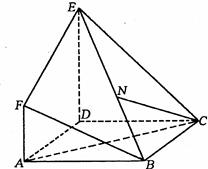 如图,在多面体ABCDEF中,底面ABCD是正方形,AF⊥平面ABCD,DE∥AF,AB=DE=2
如图,在多面体ABCDEF中,底面ABCD是正方形,AF⊥平面ABCD,DE∥AF,AB=DE=2