题目内容
已知函数f(x)=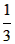 x3-
x3-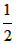 (a+1)x2-4(a+5)x,g(x)=5lnx+
(a+1)x2-4(a+5)x,g(x)=5lnx+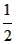 ax2-x+5,其中a∈R。
ax2-x+5,其中a∈R。
(Ⅰ)若函数f(x),g(x)有相同的极值点,求a的值;
(Ⅱ)若存在两个整数m,n,使得函数f(x),g(x)在区间(m,n)上都是减函数.求n的最大值,及n取最大值时a的取值范围。
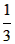 x3-
x3-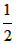 (a+1)x2-4(a+5)x,g(x)=5lnx+
(a+1)x2-4(a+5)x,g(x)=5lnx+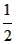 ax2-x+5,其中a∈R。
ax2-x+5,其中a∈R。(Ⅰ)若函数f(x),g(x)有相同的极值点,求a的值;
(Ⅱ)若存在两个整数m,n,使得函数f(x),g(x)在区间(m,n)上都是减函数.求n的最大值,及n取最大值时a的取值范围。
解:(Ⅰ)由已知得 f'(x)=x2-(a+1)x-4(a+5),
g'(x)=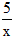 +ax-1=
+ax-1=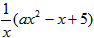
令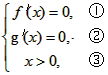
由①得x=-4或x=a+5,
由③知,只能a+5>0,即a>-5,
把x=a+5代人②,
解得a=0或a=-4或a=-6(舍去),
经检验,当a=0或a=-4时,函数f(x),g(x)有相同的极值点,
所以,a的值为0或-4;
(Ⅱ)由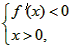 得
得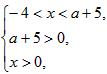 得
得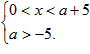 ,
,
设g'(x)<0,即ax2-x+5<0的解集为M,及 N=(0,a+5),
则由题意得区间(m,n)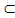 M∩N,
M∩N,
令h(x)=ax2-x+5,
①当a<0时,因为h(0)=5>0,
故只能h(a+5)=a[(a+5)2-1] <0,
即a>-4或a<-6,又因为a>-5,
故-4<a<0,此时n≤a+5<5,
又m,n∈Z,所以m<n≤4,
当且仅当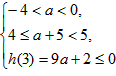 ,即-1≤a≤
,即-1≤a≤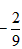 时,n可以取4,
时,n可以取4,
所以,n的最大整数为4;
②当a=0时,M∩N=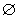 ,不合题意;
,不合题意;
③当a>0时,因为,h(0)=5>0,
h(a+5)=a[(a+5)2-1]>0,
故只能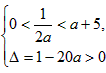 ,无解,
,无解,
综上,n的最大整数为4,此时a的取值范围为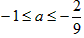 。
。
g'(x)=
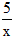 +ax-1=
+ax-1=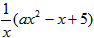
令
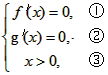
由①得x=-4或x=a+5,
由③知,只能a+5>0,即a>-5,
把x=a+5代人②,
解得a=0或a=-4或a=-6(舍去),
经检验,当a=0或a=-4时,函数f(x),g(x)有相同的极值点,
所以,a的值为0或-4;
(Ⅱ)由
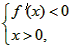 得
得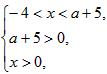 得
得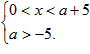 ,
,设g'(x)<0,即ax2-x+5<0的解集为M,及 N=(0,a+5),
则由题意得区间(m,n)
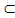 M∩N,
M∩N,令h(x)=ax2-x+5,
①当a<0时,因为h(0)=5>0,
故只能h(a+5)=a[(a+5)2-1] <0,
即a>-4或a<-6,又因为a>-5,
故-4<a<0,此时n≤a+5<5,
又m,n∈Z,所以m<n≤4,
当且仅当
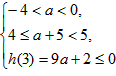 ,即-1≤a≤
,即-1≤a≤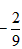 时,n可以取4,
时,n可以取4,所以,n的最大整数为4;
②当a=0时,M∩N=
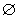 ,不合题意;
,不合题意; ③当a>0时,因为,h(0)=5>0,
h(a+5)=a[(a+5)2-1]>0,
故只能
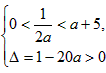 ,无解,
,无解,综上,n的最大整数为4,此时a的取值范围为
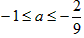 。
。 
练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|