Question

设椭圆中心在坐标原点，焦点在x轴上，一个顶点为(

2

，0)，离心率为

2

2

．
（Ⅰ）求椭圆的方程；
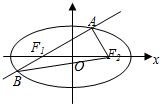
（Ⅱ）若椭圆左焦点为F₁，右焦点为F₂，过F₁且斜率为k的直线交椭圆于A、B，且|

F2A

+

F2B

|=

2 26

3

，求直线AB的方程．

Answer 1

分析：（Ⅰ）一个顶点为(

2

，0)，即a=

2

，离心率为

2

2

，可得c=1，再由a²=b²+c²，可得b=1，从而的椭圆方程
（Ⅱ）设M（x₁，y₁），N（x₂，y₂），直线AB的方程为 y=k（x+1）代入椭圆方程，得（1+2k²）x²+4k²x+2k²-2=0，从而得x₁+x₂、x₁x₂、y₁+y₂，而|

F2A

+

F2B

|=

2 26

3

即

(x1+x2-2)2+(y1+y2)2

=

2 26

3

，代入可得方程，解之即得k值

解答：解：（I）由已知得，解得a=

2

，c=1
∴b=

a2-c2

=1
∴所求椭圆的方程为

x2

2

+y2=1          
（II）由（I）得F₁（-1，0），F₂（1，0）
直线AB的方程为 y=k（x+1），
设M（x₁，y₁），N（x₂，y₂），
联立

y=k(x+1) x2 2 +y2=1

，消元得（1+2k²）x²+4k²x+2k²-2=0
∴x₁+x₂=

-4k2

1+2k2

，x₁x₂=

2k2-2

1+2k2

，
∴y₁+y₂=k（x₁+x₂+2）=

2k

1+2k2

，
又∵

F2A

=(x1-1，y1)，

F2B

=(x2-1，y2)
∴

F2A

+

F2B

=(x1+x2-2，y1+y2)
∴|

F2A

+

F2B

|=

(x1+x2-2)2+(y1+y2)2

=

2 26

3

代入x₁+x₂与y₁+y₂的值
化简得40k⁴-23k²-17=0
解得k²=1或k²=-

17

40

（舍去）
∴k=±1
∴所求直线l的方程为y=x+1或y=-x-1

点评：本题考察了椭圆的标准方程，直线与椭圆相交的关系，解题时要特别体会韦达定理在解题中的重要作用，设而不求的解题思想