题目内容
选修4-1:几何证明选讲
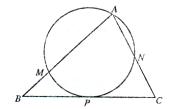
如图,已知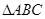 ,过顶点
,过顶点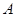 的圆与边
的圆与边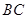 切于
切于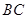 的中点
的中点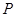 ,与边
,与边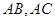 分别交于点
分别交于点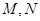 ,且
,且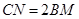 ,点
,点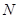 平分
平分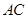 .求证:
.求证: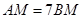 .
.
如图,已知
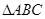 ,过顶点
,过顶点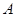 的圆与边
的圆与边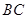 切于
切于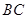 的中点
的中点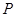 ,与边
,与边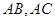 分别交于点
分别交于点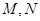 ,且
,且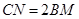 ,点
,点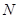 平分
平分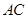 .求证:
.求证: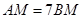 .
.
见解析。
本题考查与圆有关的比例线段的求法,解题时要认真审题,注意切割线定理的合理运用.
由切、割线定理,得BP2=BM•BA,CP2=CN•CA,由BP=CP,知BM•BA=2CN2,由CN=NA=2BM,BA=BM+AM,能够证明AM=7BM.
证法一:连结PM、PA、PN
∵BP是圆的切线,∴∠BPM=∠BAP,∠CPN=∠CAP
∴△BPM∽△BAP,△CPN∽△CAP
∴ ,……5分
,……5分
即
∵ ,∴
,∴ ,
,
∵ ,∴
,∴ ,
,
∴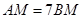 ……10分
……10分
证法二:由切、割线定理,得 ,……5分
,……5分
∵ ,∴
,∴ ,
,
∵ ,∴
,∴ ,
,
∴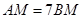 ……10分
……10分
由切、割线定理,得BP2=BM•BA,CP2=CN•CA,由BP=CP,知BM•BA=2CN2,由CN=NA=2BM,BA=BM+AM,能够证明AM=7BM.
证法一:连结PM、PA、PN
∵BP是圆的切线,∴∠BPM=∠BAP,∠CPN=∠CAP
∴△BPM∽△BAP,△CPN∽△CAP
∴
 ,……5分
,……5分即

∵
 ,∴
,∴ ,
,∵
 ,∴
,∴ ,
,∴
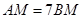 ……10分
……10分证法二:由切、割线定理,得
 ,……5分
,……5分∵
 ,∴
,∴ ,
,∵
 ,∴
,∴ ,
,∴
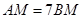 ……10分
……10分
练习册系列答案
相关题目
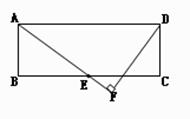
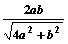
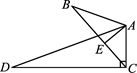
 是△
是△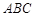 的外接圆,D是的中点,BD交AC于E.
的外接圆,D是的中点,BD交AC于E.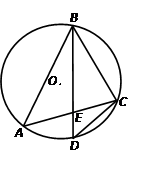
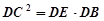 ;
;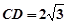 ,O到AC的距离为1,求⊙O的半径
,O到AC的距离为1,求⊙O的半径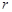 .
.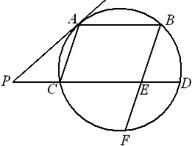
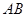 和
和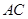 是圆的两条弦,过点
是圆的两条弦,过点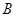 作圆的切线与
作圆的切线与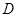 .过点
.过点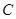 作
作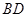 的平行线与圆交于点
的平行线与圆交于点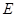 ,与
,与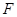 ,
,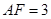 ,
,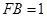 ,
,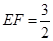 ,则线段
,则线段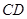 的长为 .
的长为 .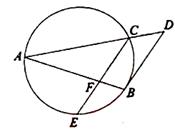
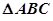 是圆O的内接三角形,圆O的半径
是圆O的内接三角形,圆O的半径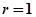 ,
,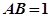 ,
,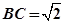 ,
,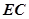 是圆
是圆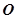 的切线,则
的切线,则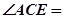 _______.
_______.
 为△
为△ 的外心,
的外心,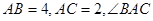 为钝角,
为钝角, 是边
是边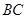 的中点,则
的中点,则 的值 ( ).
的值 ( ).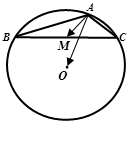
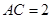 ,则BD等于 .
,则BD等于 .