题目内容
已知圆C: .直线
.直线 过点P(1,2),且与圆C交于A.B两点,若|AB|=
过点P(1,2),且与圆C交于A.B两点,若|AB|=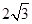 ,则直线
,则直线 的方程_____
___ .
的方程_____
___ .
【答案】
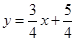 或
或
【解析】
试题分析:分两种情况考虑:
(i)当直线l的斜率不存在时(或直线l与x轴垂直),
由P(1,2),得到直线l为x=1,
该直线与圆x2+y2=4相交于两点A(1,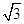 ),B(1,-
),B(1,-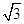 ),
),
满足|AB|=2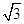 ,符合题意;
,符合题意;
(ii)当直线l的斜率存在时,设直线l的斜率为k,
由P(1,2),得到直线l方程为y-2=k(x-1),即kx-y+(2-k)=0,
由圆的方程x2+y2=4,得到圆心坐标为(0,0),半径r=2,
∴圆心到直线l的距离d=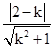 ,又|AB|=2
,又|AB|=2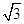 ,
,
∴d2+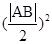 =r2,即(
=r2,即(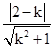 )2+(
)2+(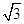 )2=4,
)2=4,
整理得:-4k=-3,解得:k= ,
,
此时直线l的方程为
 x-y+(2-
x-y+(2- )=0,即3x-4y+5=0,
)=0,即3x-4y+5=0,
综上知,直线l的方程为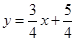 或
或 。
。
考点:本题主要考查直线与圆的位置关系,直线的点斜式方程,圆的标准方程,勾股定理,垂径定理,以及点到直线的距离公式。
点评:中档题,利用分类讨论的思想,当直线与圆相交时,常常根据垂径定理由垂直得中点,进而由弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理来解答。

练习册系列答案
相关题目