题目内容
已知函数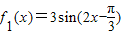 ,
,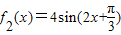 ,则函数f(x)=f1(x)+f2(x)的振幅为( )
,则函数f(x)=f1(x)+f2(x)的振幅为( )A.
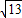
B.5
C.7
D.13
【答案】分析:利用两角和的正弦函数直接化简f(x)为一个角的一个三角函数的形式,即可求出函数的振幅.
解答:解:函数f(x)=f1(x)+f2(x)
=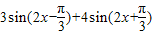
=3sin2xcos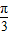 -3cos2xsin
-3cos2xsin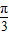 +4sin2xcos
+4sin2xcos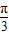 +4cos2xsin
+4cos2xsin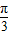
=7sin2xcos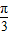 +cos2xsin
+cos2xsin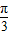
= sin2x+
sin2x+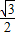 cos2x
cos2x
=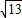 sin(2x+θ).其中tanθ=
sin(2x+θ).其中tanθ=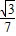 .
.
所以函数的振幅为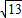 .
.
故选A.
点评:本题考查两角和的正弦函数的应用,三角函数的恒等变形,考查计算能力.
解答:解:函数f(x)=f1(x)+f2(x)
=
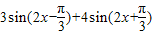
=3sin2xcos
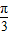 -3cos2xsin
-3cos2xsin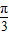 +4sin2xcos
+4sin2xcos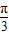 +4cos2xsin
+4cos2xsin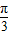
=7sin2xcos
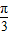 +cos2xsin
+cos2xsin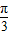
=
 sin2x+
sin2x+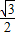 cos2x
cos2x=
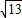 sin(2x+θ).其中tanθ=
sin(2x+θ).其中tanθ=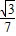 .
.所以函数的振幅为
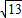 .
.故选A.
点评:本题考查两角和的正弦函数的应用,三角函数的恒等变形,考查计算能力.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目