题目内容
【题目】如图5，在四棱锥P-ABCD中，PA⊥平面ABCD，AB=4，BC=3，AD=5，∠DAB=∠ABC=90°，E是CD的中点.
（Ⅰ）证明：CD⊥平面PAE；
（Ⅱ）若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等，求四棱锥P-ABCD的体积.
【答案】（1）证明略
（2）
【解析】
解法1（Ⅰ如图（1）），连接AC，由AB=4，
，
Ｅ是ＣＤ的中点，所以
所以
而
内的两条相交直线，所以CD⊥平面PAE.
（Ⅱ）过点Ｂ作
由（Ⅰ）CD⊥平面PAE知，ＢＧ⊥平面PAE.于是
为直线ＰＢ与平面PAE
所成的角，且
.
由
知，
为直线
与平面
所成的角.
由题意，知
因为
所以
由
所以四边形
是平行四边形，故
于是
在
中，
所以
于是
又梯形
的面积为
所以四棱锥
的体积为
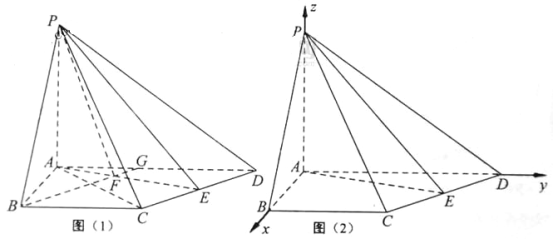
解法2：如图（2），以A为坐标原点，
所在直线分别为
建立空间直角坐标系.设
则相关的各点坐标为：
（Ⅰ）易知
因为
所以
而
是平面
内的两条相交直线，所以
(Ⅱ)由题设和（Ⅰ）知，
分别是
，
的法向量，而PB与
所成的角和PB与所成的角相等，所以
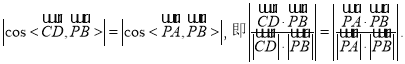
由（Ⅰ）知，
由
故
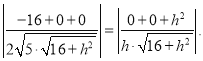
解得
.又梯形ABCD的面积为
，所以四棱锥
的体积为.
【题目】甲，乙两台机床同时生产一种零件，其质量按测试指标划分：指标大于或等于100为优品，大于等于90且小于100为合格品，小于90为次品，现随机抽取这两台车床生产的零件各100件进行检测，检测结果统计如下：
测试指标 |
|
|
|
|
|
机床甲 | 8 | 12 | 40 | 32 | 8 |
机床乙 | 7 | 18 | 40 | 29 | 6 |
（1）试分别估计甲机床、乙机床生产的零件为优品的概率；
（2）甲机床生产一件零件，若是优品可盈利160元，合格品可盈利100元，次品则亏损20元；假设甲机床某天生产50件零件，请估计甲机床该天的日利润（单位：元）；
（3）从甲、乙机床生产的零件指标在
内的零件中，采用分层抽样的方法抽取5件，从这5件中任选2件进行质量分析，求这2件都是乙机床生产的概率.
