Question

【题目】如图，已知， ，且是的中点，.

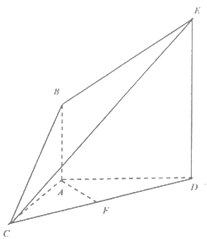
（1）求证：；

（2）求证：平面平面；

（3）求与平面所成角的正弦值.

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）。

【解析】

（1）取的中点，可以利用中位线定理，根据已知的平行关系和长度关系，可以得到一个平行四边形，利用平行四边形的对边平行，这样得到线线平行，也就能证明出线面平行；

（2）通过已知和（1）可知，通过线面垂直和平行线的性质，可以这样可以证明出线面垂直，而从而证明出平面利用面面垂直的判定定理可以证明出平面平面；

（3）通过（2）证明出的线面垂直关系，找到线面角，利用勾股定理、平行四边形的性质，求出相关的边，利用正弦的定义，求出与平面所成角的正弦值。

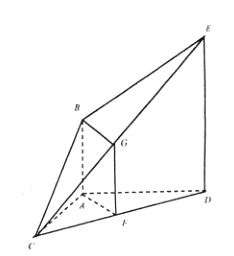
（1）如上图，取的中点，连接,

由是的中点，且又，且

且. 是平行四边形，从而，

又平面，平面, 因此；

（2）证明：是的中点，，

因为平面，，所以平面，

又平面 而 平面

由可知平面 平面，平面平面；

（3）由（2）知平面 是在平面的射影，则与平面所成的角为，因为，所以,由（1）可知：

是平行四边形，从而，

在中，

与平面所成角的正弦值是。