题目内容
求双曲线y=
解:由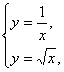 得
得![]() 得两曲线交点坐标为(1,1).于是双曲线y=
得两曲线交点坐标为(1,1).于是双曲线y=![]() 在(1,1)处的切线斜率k1=-1,抛物线y=
在(1,1)处的切线斜率k1=-1,抛物线y=![]() 在点(1,1)处的切线斜率k2=
在点(1,1)处的切线斜率k2=![]() .设两切线的夹角为α,则tanα=|
.设两切线的夹角为α,则tanα=|![]() |=3.因此所求的两切线夹角为α=arctan3.
|=3.因此所求的两切线夹角为α=arctan3.

练习册系列答案
相关题目
题目内容
求双曲线y=
解:由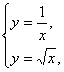 得
得![]() 得两曲线交点坐标为(1,1).于是双曲线y=
得两曲线交点坐标为(1,1).于是双曲线y=![]() 在(1,1)处的切线斜率k1=-1,抛物线y=
在(1,1)处的切线斜率k1=-1,抛物线y=![]() 在点(1,1)处的切线斜率k2=
在点(1,1)处的切线斜率k2=![]() .设两切线的夹角为α,则tanα=|
.设两切线的夹角为α,则tanα=|![]() |=3.因此所求的两切线夹角为α=arctan3.
|=3.因此所求的两切线夹角为α=arctan3.
