题目内容
(2009年)若函数y=
ax3-
ax2-2ax(a≠0)在[-1,2]上为增函数,则实数a的取值范围是______.
| 1 |
| 3 |
| 1 |
| 2 |
y′=ax2-ax-2a,
因为函数y=
ax3-
ax2-2ax(a≠0)在[-1,2]上为增函数,
所以ax2-ax-2a≥0在[-1,2]上恒成立,
即a(x-2)(x+1)≥0在[-1,2]上恒成立,
所以a<0,
故答案为:a<0.
因为函数y=
| 1 |
| 3 |
| 1 |
| 2 |
所以ax2-ax-2a≥0在[-1,2]上恒成立,
即a(x-2)(x+1)≥0在[-1,2]上恒成立,
所以a<0,
故答案为:a<0.

练习册系列答案
相关题目
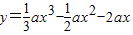 (a≠0)在[-1,2]上为增函数,则实数a的取值范围是 .
(a≠0)在[-1,2]上为增函数,则实数a的取值范围是 .