题目内容

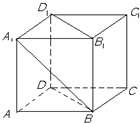精英家教网如图ABCD-A1B1C1D1是棱长为a的正方体，则AB1与平面D1B1BD所成角=
 
．
分析：连接A1C1，交B1D1于O，根据正方体的几何特征及线面夹角的定义，我们呆得∠A1BO即为AB1与平面D1B1BD所成角，解三角形A1BO，即可求出AB1与平面D1B1BD所成角．
解答：解：连接A1C1，交B1D1于O，
由正方体的几何特征易得，A1O⊥平面D1B1BD
连接BO，则∠A1BO即为AB1与平面D1B1BD所成角
又∵ABCD-A1B1C1D1是棱长为a的正方体，
∴A1B=
2
a，BO=
6
2
a，A10=
2
2
a
则cos∠A1BO=
A1O
A1B
=
1
2

∴∠A1BO=
π
3

故答案为：
π
3
．
点评：本题考查的知识点是直线与平面所成的角，其中根据已知条件求出AB1与平面D1B1BD所成角的平面角为∠A1BO是解答本题的关键．
练习册系列答案
相关题目
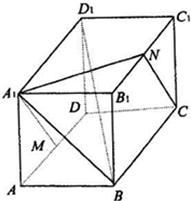
精英家教网如图，长方体ABCD-A1B1C1D1中，AB=A1A=a，BC=
2
a，M是AD中点，N是B1C1中点．
（1）求证：A1、M、C、N四点共面；
（2）求证：BD1⊥MCNA1；
（3）求证：平面A1MNC⊥平面A1BD1；
（4）求A1B与平面A1MCN所成的角．
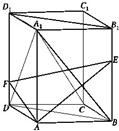精英家教网如图，在长方体ABCD-A1B1C1D1中，点E、F分别BB1、DD1上，且AE⊥A1B，AF⊥A1D．
（1）求证：A1C⊥平面AEF；
（2）若规定两个平面所成的角是这两个平面所组成的二面角中的锐角（或直角），则在空间中有定理：若两条直线分别垂直于两个平面，则这两条直线所成的角与这两个平面所成的角相等．
试根据上述定理，在AB=4，AD=3，AA1=5时，求平面AEF与平面D1B1BD所成的角的大小．（用反三角函数值表示）
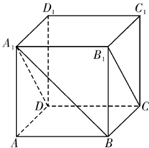精英家教网如图，在正方体ABCD-A1B1C1D1中，棱长为a，M、N分别为A1B和AC上的点，A1M=AN=
2
a
3
，则MN与平面BB1C1C的位置关系是（　　）
A、相交B、平行
C、垂直D、不能确定
精英家教网如图，在正方体ABCD-A1B1C1D1中，直线A1B与平面A1B1CD所成的角的大小等于
 
．
（2007•无锡二模）如图，已知四棱柱ABCD-A1B1C1D1的底面ABCD为直角梯形，AB∥CD，AB⊥AD，AB=AD=A1B=2CD，侧面A1ADD1为正方形．
（1）求直线A1A与底面ABCD所成角的大小；
（2）求二面角C-A1B-A正切值的大小；
（3）在棱C1C上是否存在一点P，使得 D1P∥平面A1BC，若存在，试说明点P的位置；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网