题目内容
 正四棱柱ABCD-A1B1C1D1中,AB=2,A1A=2
正四棱柱ABCD-A1B1C1D1中,AB=2,A1A=2| 2 |
(1)求证:A1C⊥平面BEF;
(2)求二面角A1-BF-E的大小.
分析:(1)建立如图所示的空间直角坐标系A-xyz,分别求出
,
,
,根据
•
=0,
•
=0可得A1C⊥BE,A1C⊥BF,结合线面垂直的判定定理可得A1C⊥平面BEF;
(2)由(1)可得
=(2,2,-2
)是平面BEF的一个法向量,出平面A1BF的一个法向量,代入向量夹角公式,即可求出二面角A1-BF-E的大小.
| A1C |
| BE |
| BF |
| A1C |
| BE |
| A1C |
| BF |
(2)由(1)可得
| A1C |
| 2 |
解答: 解:建立如图所示的空间直角坐标系A-xyz,
解:建立如图所示的空间直角坐标系A-xyz,
∵正四棱柱ABCD-A1B1C1D1中,AB=2,A1A=2
,设E,F分别是BD,C1C的中点
∴A(0,0,0),A1(0,0,2
),B(2,0,0),C(2,2,0),E(1,1,0),F(2,2,
),
∴
=(2,2,-2
),
=(-1,1,0),
=(0,2,
),
∵
•
=0,
•
=0
∴A1C⊥BE,A1C⊥BF,
又∵BE∩BF=B
∴A1C⊥平面BEF;
(2)由(1)可得
=(2,2,-2
)是平面BEF的一个法向量
且
=(2,0,-2
),
设向量
=(a,b,c)是平面A1BF的一个法向量
则
即
令c=2,则
=(2
,-
,2)是平面A1BF的一个法向量
令锐二面角A1-BF-E的平面角为θ
则cosθ=
=
=
故二面角A1-BF-E的大小为arccos
 解:建立如图所示的空间直角坐标系A-xyz,
解:建立如图所示的空间直角坐标系A-xyz,∵正四棱柱ABCD-A1B1C1D1中,AB=2,A1A=2
| 2 |
∴A(0,0,0),A1(0,0,2
| 2 |
| 2 |
∴
| A1C |
| 2 |
| BE |
| BF |
| 2 |
∵
| A1C |
| BE |
| A1C |
| BF |
∴A1C⊥BE,A1C⊥BF,
又∵BE∩BF=B
∴A1C⊥平面BEF;
(2)由(1)可得
| A1C |
| 2 |
且
| A1B |
| 2 |
设向量
| m |
则
|
即
|
令c=2,则
| m |
| 2 |
| 2 |
令锐二面角A1-BF-E的平面角为θ
则cosθ=
|
| ||||
|
|
2
| ||
4•
|
| ||
| 14 |
故二面角A1-BF-E的大小为arccos
| ||
| 14 |
点评:本题考查的知识点是二面角的平面角及求法,直线与平面垂直的判定,其中建立空间坐标系,将空间线面关系及二面角的大小转化为向量垂直及夹角问题是解答的关键.

练习册系列答案
相关题目
顶点在同一球面上的正四棱柱ABCD-A′B′C′D′中,AB=1,AA′=
,则A、C两点间的球面距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
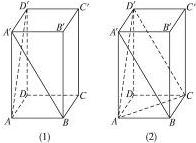 如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是
如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是