题目内容
正三棱锥的底面边长为a,侧棱与底面成45°角,求此棱锥的侧面积.
解:如图,作SO⊥平面ABC于O(O为△ABC的中心),连结AO交BC于D,则AD⊥BC,由三垂线定理知SD⊥BC.
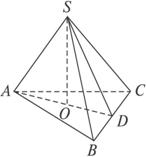
∴SD为斜高,∠SAD=45°.
∵AD=![]() ,
,
∴AO=![]() AD=
AD=![]() ,SO=AOtan45°=
,SO=AOtan45°=![]() .
.
又∵OD=![]() AD=
AD=![]() ,
,
∴![]() .
.
∴S侧=![]() ·3a·
·3a·![]() .
.
另解: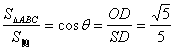 ,
,
∴S侧=![]() S△ABC=
S△ABC=![]() .
.

练习册系列答案
相关题目
正三棱锥的底面边长为a,高为
a,则此棱锥的侧面积等于( )
| ||
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|