题目内容
 如图,平面内有三个向量:
如图,平面内有三个向量:| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| c |
| a |
| b |
| b |
| c |
| a |
| b |
| c |
| 3 |
| c |
| a |
| b |
分析:由题设条件,本题是一个根据利用向量运算求参数题,可通过构建方程求m,b的值,由题意其中
与
的夹角为30°,
与
的夹角为120°,
⊥
,可对
=m•
+n•
两边分别点乘向量
消去n求得m,再将m的值代回,得到
=4•
+n•
,然后两边点乘
得到n的方程求出n的值
| a |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
| b |
| c |
| c |
| a |
| b |
| b |
解答:解:由题意得:
•
=3,
•
=-
•
=0
由
=m
+n
得
2=m
•
+n
•
即12=m×2
×
,解得m=4
同理,
=4•
+n•
得
•
=4
•
+n
2
即0=4×(-
)+n,得n=2
综上,m=4,n=2
| a |
| c |
| a |
| b |
| 1 |
| 2 |
| c |
| b |
由
| c |
| a |
| b |
得
| c |
| a |
| c |
| b |
| c |
即12=m×2
| 3 |
| ||
| 2 |
同理,
| c |
| a |
| b |
得
| c |
| b |
| a |
| b |
| b |
即0=4×(-
| 1 |
| 2 |
综上,m=4,n=2
点评:本题考查平面向量数量积的运算,解题的关键是理解题意,通过对向量方程两边点乘不同的向量得到m,n的方程从而求得两个参数的值,本题采用两边点乘向量的技巧得到参数的方程,是向量中独有的运算方式,注意总结其变形原理

练习册系列答案
相关题目
 如图,设Ox,Oy是平面内相交成60°角的两条数轴,
如图,设Ox,Oy是平面内相交成60°角的两条数轴, ,
, 分别是与x轴,y轴正方向同向的单位向量,若向量
分别是与x轴,y轴正方向同向的单位向量,若向量 =x
=x +y
+y ,则把有序数对(x,y)叫做向量
,则把有序数对(x,y)叫做向量 在坐标系xOy中的坐标.设
在坐标系xOy中的坐标.设 ,
, ,给出下列三个命题:
,给出下列三个命题: =(1,0);
=(1,0);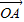 ⊥
⊥ ;
;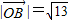 .
.