题目内容
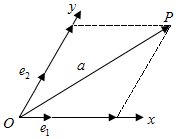
如图，设Ox，Oy是平面内相交成60°角的两条数轴，| e1 |
| e2 |
| OP |
| e1 |
| e2 |
| OP |
| OA |
| OB |
①
| e1 |
②
| OA |
| e1 |
③|
| OB |
| 13 |
其中，真命题的编号是
①②
①②
．（写出所有真命题的编号）分析：由平面向量基本定理，结合题意得到①正确；由题意算出
•
═
且
2=
2=1，从而得到
•
=（-
+2
）•
=0，得
⊥
，得②正确；同理算出
2=（3
+2
）2=19，得到|
|=
，故③不正确．由此可得本题答案．
| e1 |
| e2 |
| 1 |
| 2 |
| e1 |
| e2 |
| OA |
| e1 |
| e1 |
| e2 |
| e1 |
| OA |
| e1 |
| OB |
| e1 |
| e2 |
| OB |
| 19 |
解答：解：∵
=x
+y
，当且仅当x=1、y=0
∴向量
的坐标为（1，0），即
=（1，0），故①正确；
∵
•
=|
|•|
|cos60°=
，
2=
2=1
∴
•
=（-
+2
）•
=-
2+2
•
=-1+2×
=0
可得
⊥
，得②正确；
∵
=(3，2)=3
+2
∴
2=（3
+2
）2=9
2+12
•
+4
2=9+6+4=19
∴|
|=
=
，故③不正确
综上所述，真命题的编号为①②
故答案为：①②
| e1 |
| e1 |
| e2 |
∴向量
| e1 |
| e1 |
∵
| e1 |
| e2 |
| e1 |
| e2 |
| 1 |
| 2 |
| e1 |
| e2 |
∴
| OA |
| e1 |
| e1 |
| e2 |
| e1 |
| e1 |
| e2 |
| e1 |
| 1 |
| 2 |
可得
| OA |
| e1 |
∵
| OB |
| e1 |
| e2 |
∴
| OB |
| e1 |
| e2 |
| e1 |
| e1 |
| e2 |
| e2 |
∴|
| OB |
|
| 19 |
综上所述，真命题的编号为①②
故答案为：①②
点评：本题给出斜坐标系，判断几个命题的真假性．着重考查了向量数量积的定义和运算性质、平面向量基本定理等知识，属于中档题．
练习册系列答案
相关题目
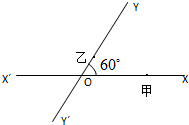如图，有两条相交成60°的直路XX′，YY′，交点是O，甲、乙分别在OX，OY上，起初甲离O点3km，乙离O点1km，后甲沿XX′方向用2km/h的速度，乙沿Y′Y方向用4km/h的速度同时步行．设t小时后甲在XX′上点A处，乙在YY′上点B处．
、
分别是与x轴、y轴正方向同向的单位向量，若向量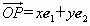
，则把有序数对(x，y)叫做向量
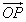在坐标系xOy中的坐标．假设
，
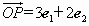的大小；
如图，有两条相交成60°的直路XX′，YY′，交点是O，甲、乙分别在OX，OY上，起初甲离O点3km，乙离O点1km，后甲沿XX′方向用2km/h的速度，乙沿Y′Y方向用4km/h的速度同时步行．设t小时后甲在XX′上点A处，乙在YY′上点B处．
，
分别是与x轴，y轴正方向同向的单位向量，若向量
=x
+y
，则把有序数对（x，y）叫做向量
在坐标系xOy中的坐标．设
，
，给出下列三个命题：
=（1，0）；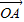
⊥
；
．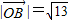