题目内容
设集合A中不含有元素-1,0,1,且满足条件:若a∈A,则有
∈A,请考虑以下问题:
(1)已知2∈A,求出A中其它所有元素;
(2)自己设计一个实数属于A,再求出A中其它所有元素;
(3)根据已知条件和前面(1)(2)你能悟出什么道理来,并证明你的猜想.
| 1+a | 1-a |
(1)已知2∈A,求出A中其它所有元素;
(2)自己设计一个实数属于A,再求出A中其它所有元素;
(3)根据已知条件和前面(1)(2)你能悟出什么道理来,并证明你的猜想.
分析:(1)由题中条件:集合A中不含有元素-1,0,1,且满足条件:若a∈A,则有
∈A,得集合A中元素为2,-3,-
,
;
(2)任取一常数,如3∈A,同(1)可得A={3,-2,-
,
};
(3)由(1)(2)猜想,A={a,
,-
,
},给出证明即可.
| 1+a |
| 1-a |
| 1 |
| 2 |
| 1 |
| 3 |
(2)任取一常数,如3∈A,同(1)可得A={3,-2,-
| 1 |
| 3 |
| 1 |
| 2 |
(3)由(1)(2)猜想,A={a,
| 1+a |
| 1-a |
| 1 |
| a |
| a-1 |
| a+1 |
解答:解:(1)∵2∈A,由题中条件:集合A中不含有元素-1,0,1,且满足条件:若a∈A,则有
∈A,得
=-3∈A.
∵-3∈A,∴
=-
∈A.∵-
∈A,∴
=
∈A.∵
∈A,∴
=2∈A.
∴集合A={2,-3,-
,
}.
(2)任取一常数,如3∈A,则同理(1)可得:集合A={3,-2,-
,
}.
(3)由(1)(2)猜想:任意的常数a∈A(a≠±1,a≠0),则集合A={a,
,-
,
}.
证明:∵a∈A,∴
∈A,∴
=-
,
∴
=
∈A,∴
=a∈A.
如果其中任两元素相等,则a=±1或a=0,故这四个元素不等(集合中元素的互异性).
| 1+a |
| 1-a |
| 1+2 |
| 1-2 |
∵-3∈A,∴
| 1-3 |
| 1+3 |
| 1 |
| 2 |
| 1 |
| 2 |
1-
| ||
1+
|
| 1 |
| 3 |
| 1 |
| 3 |
1+
| ||
1-
|
∴集合A={2,-3,-
| 1 |
| 2 |
| 1 |
| 3 |
(2)任取一常数,如3∈A,则同理(1)可得:集合A={3,-2,-
| 1 |
| 3 |
| 1 |
| 2 |
(3)由(1)(2)猜想:任意的常数a∈A(a≠±1,a≠0),则集合A={a,
| 1+a |
| 1-a |
| 1 |
| a |
| a-1 |
| a+1 |
证明:∵a∈A,∴
| 1+a |
| 1-a |
1+
| ||
1-
|
| 1 |
| a |
∴
1-
| ||
1+
|
| a-1 |
| a+1 |
1+
| ||
1-
|
如果其中任两元素相等,则a=±1或a=0,故这四个元素不等(集合中元素的互异性).
点评:本题考查元素与集合的关系,属于基础题.关键是审题时要注意:集合A中不含有元素-1,0,1,且满足条件:若a∈A,则有
∈A,得集合A={a,
,-
,
}.
| 1+a |
| 1-a |
| 1+a |
| 1-a |
| 1 |
| a |
| a-1 |
| a+1 |

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 ,且满足条件:若
,且满足条件:若 ,则有
,则有 ,
, ,求出A中其它所有元素;
,求出A中其它所有元素;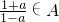 ,请考虑以下问题:
,请考虑以下问题: