题目内容
两个圆C1:x2+y2-4y=0与圆C2:x2+8x+y2+7=0的位置关系是________.
相交
分析:将圆化为标准方程,利用圆心距与半径和差之间的关系,即可得到结论.
解答:圆C1:x2+y2-4y=0的标准方程为x2+(y-2)2=4,C1(0,2),半径为2;
圆C2:x2+8x+y2+7=0的标准方程为(x+4)2+y2=9,C2(-4,0),半径为3,
∴|C1C2|=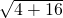 =2
=2
∵3-2< <3+2
<3+2
∴两圆相交
故答案为:相交.
点评:本题考查圆的方程,考查两圆的位置关系,考查学生的计算能力,属于基础题.
分析:将圆化为标准方程,利用圆心距与半径和差之间的关系,即可得到结论.
解答:圆C1:x2+y2-4y=0的标准方程为x2+(y-2)2=4,C1(0,2),半径为2;
圆C2:x2+8x+y2+7=0的标准方程为(x+4)2+y2=9,C2(-4,0),半径为3,
∴|C1C2|=
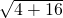 =2
=2
∵3-2<
 <3+2
<3+2∴两圆相交
故答案为:相交.
点评:本题考查圆的方程,考查两圆的位置关系,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
 下列命题正确的有
下列命题正确的有
 上的点,过点P作圆C1的一条切线,切点为T1,过点P作圆C2的一条切线,切点为T2,问:是否存在点P,使无穷多个圆C2,满足PT1=PT2?如果存在,求出所有这样的点P;如果不存在,说明理由.
上的点,过点P作圆C1的一条切线,切点为T1,过点P作圆C2的一条切线,切点为T2,问:是否存在点P,使无穷多个圆C2,满足PT1=PT2?如果存在,求出所有这样的点P;如果不存在,说明理由.