Question

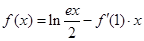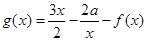已知函数，（其中）.

（1）求的单调区间；

（2）若函数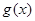在区间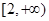上为增函数，求的取值范围；

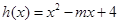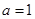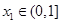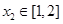（3）设函数，当时，若存在，对任意的，总有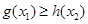成立，求实数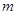的取值范围.

 

Answer 1

【答案】

（1）的单调增区间为，单调减区间为.

（2）

（3））

【解析】

试题分析：解：（1），，

，故.

当时，；当时，.

的单调增区间为，单调减区间为.……3分

（2），则，由题意可知在上恒成立，即在上恒成立，因函数开口向上，且对称轴为，故在上单调递增，因此只需使，解得；

易知当时，且不恒为0.

故.……7分

（3）当时，，，故在上，即函数在上单调递增，.……9分

而“存在，对任意的，总有成立”等价于“在上的最大值不小于在上的最大值”.

而在上的最大值为中的最大者，记为.

所以有，，

.

故实数的取值范围为.……13分

考点：导数的运用

点评：主要是考查了导数在研究函数中的运用，属于中档题。