题目内容
如图所示，某市（A）有四个郊县（B、C、D、E），现备有5种颜色，问有多少种不同的涂色方式，使每相邻两块不同色，每块只涂一种颜色?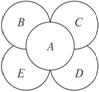
解：完成这件事分三类：第一类：用五种颜色涂，共有A
=120种不同方法.第二类:用四种颜色涂，选四种颜色的方法有C
种，其中选一种颜色涂A有C
种方法，剩余四块涂3种颜色.有且仅有一组不相邻区域涂同一种颜色，选一组不相邻区域的方法有2种.在余下的三种颜色中选一种颜色涂这不相邻区域有C
种方法，最后剩下两种颜色涂2个区域有A
种方法，根据乘法原理，得C
·C
·2·C
·A
=240种.第三类：用三种颜色涂，选色方法有C
种.B、C和D，E和A各涂一种颜色有A
种方法，故得C
A
=60种方法.根据加法原理，共有涂色方法120+240+60=420种.
练习册系列答案
相关题目
（2011•盐城二模）如图所示，某市准备在一个湖泊的一侧修建一条直路OC；另一侧修建一条观光大道，它的前一段OD是以O为顶点，x轴为对称轴，开口向右的抛物线的一部分，后一段DBC是函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜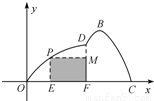
如图所示，某市准备在一个湖泊的一侧修建一条直路OC；另一侧修建一条观光大道，它的前一段OD是以O为顶点，x轴为对称轴，开口向右的抛物线的一部分，后一段DBC是函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
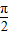），x∈[4，8]时的图象，图象的最高点为B（5，
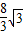），DF⊥OC，垂足为F．
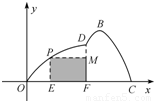如图所示，某市准备在一个湖泊的一侧修建一条直路OC；另一侧修建一条观光大道，它的前一段OD是以O为顶点，x轴为对称轴，开口向右的抛物线的一部分，后一段DBC是函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
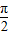），x∈[4，8]时的图象，图象的最高点为B（5，
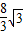），DF⊥OC，垂足为F．
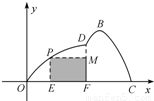如图所示，某市准备在一个湖泊的一侧修建一条直路OC；另一侧修建一条观光大道，它的前一段OD是以O为顶点，x轴为对称轴，开口向右的抛物线的一部分，后一段DBC是函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
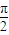），x∈[4，8]时的图象，图象的最高点为B（5，
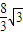），DF⊥OC，垂足为F．