题目内容
已知函数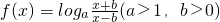 .
.
(1)求函数f(x)的定义域;
(2)判断函数的奇偶性;
(3)判断f(x)的单调性,并用定义证明.
解:(1)依题意可知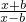 >0,又b>0,
>0,又b>0,
∴x>b或x<-b,
∴函数f(x)的定义域为(-∞,-b)∪(b,+∞);
(2)∵f(-x)+f(x)=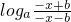 +
+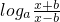
=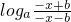 •
•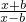
=loga1
=0,
∴函数f(x)为奇函数;
(3)∵a>1,设b<x1<x2,
则f(x1)-f(x2)=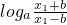 -
-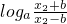
=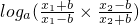 >loga1>0,
>loga1>0,
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2),
∴f(x)在(b,+∞)上的单调递减;
同理可证f(x)在(-∞,-b)上单调递减;
故f(x)在(-∞,-b)与(b,+∞)上均为减函数.
分析:(1)由对数函数的意义可知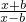 >0,从而可求函数f(x)的定义域;
>0,从而可求函数f(x)的定义域;
(2)利用f(-x)+f(x)=0可判断函数的奇偶性;
(3)设b<x1<x2,作差f(x1)-f(x2)判断其符号即可知f(x)在(b,+∞)上的单调性,同理可知f(x)在(-∞,-b)上的单调性.
点评:本题考查对数函数的定义域,考查对数函数的奇偶性与单调性,突出考查定义证明函数的单调性,属于中档题.
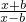 >0,又b>0,
>0,又b>0,∴x>b或x<-b,
∴函数f(x)的定义域为(-∞,-b)∪(b,+∞);
(2)∵f(-x)+f(x)=
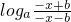 +
+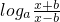
=
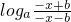 •
•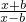
=loga1
=0,
∴函数f(x)为奇函数;
(3)∵a>1,设b<x1<x2,
则f(x1)-f(x2)=
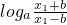 -
-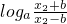
=
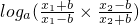 >loga1>0,
>loga1>0,∴f(x1)-f(x2)>0,
∴f(x1)>f(x2),
∴f(x)在(b,+∞)上的单调递减;
同理可证f(x)在(-∞,-b)上单调递减;
故f(x)在(-∞,-b)与(b,+∞)上均为减函数.
分析:(1)由对数函数的意义可知
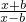 >0,从而可求函数f(x)的定义域;
>0,从而可求函数f(x)的定义域;(2)利用f(-x)+f(x)=0可判断函数的奇偶性;
(3)设b<x1<x2,作差f(x1)-f(x2)判断其符号即可知f(x)在(b,+∞)上的单调性,同理可知f(x)在(-∞,-b)上的单调性.
点评:本题考查对数函数的定义域,考查对数函数的奇偶性与单调性,突出考查定义证明函数的单调性,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.