题目内容
设函数f(x)=(1)求a,b,c的值;
(2)当x<0,f(x)的单调性如何?用单调性定义证明你的结论.
解析:(1)由f(x)= ![]() 是奇函数,得f(-x)=-f(x)对定义域内x恒成立,
是奇函数,得f(-x)=-f(x)对定义域内x恒成立,
则![]() -bx+c=-(bx+c)对定义域内x恒成立,即c=0(或由定义域关于原点对称得c=0).
-bx+c=-(bx+c)对定义域内x恒成立,即c=0(或由定义域关于原点对称得c=0).
又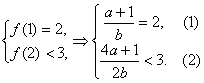
由①得a=2b-1代入得
![]() <0
<0![]() 0<b<
0<b<![]() .
.
又a,b,c是整数,得b=a=1.
(2)由(1)知,f(x)=![]() =x+
=x+![]() ,
,
当x<0,f(x)在(-∞,-1]上单调递增,在[-1,0)上单调递减.下面用定义证明之.设x1<x2≤-1,则
f(x1)-f(x2)=x1+![]() -(x2+
-(x2+![]() )=x1-x2+
)=x1-x2+![]() =(x1-x2)(1-
=(x1-x2)(1-![]() ),
),
因为x1<x2≤-1,x1-x2<0,
1-![]() >0,f(x1)-f(x2)<0,
>0,f(x1)-f(x2)<0,
故f(x)在(-∞,-1]上单调递增;
同理,可证f(x)在[-1,0)上单调递减.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目