题目内容
已知数列{an满足a1= ,且对任意n∈N*,都有
,且对任意n∈N*,都有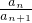 =
= .
.
(Ⅰ)求证:数列{ }为等差数列,并求{an}的通项公式;
}为等差数列,并求{an}的通项公式;
(Ⅱ)试问数列{an}中ak•ak+1是否仍是{an}中的项?如果是,请指出是数列的第几项;如果不是,请说明理由.
解:(Ⅰ)∵anan+1+2an=4anan+1+2an+1,2an-2an+1=3anan+1,
∴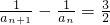 ,
,
所以数列 是
是 为首项,公差
为首项,公差 的等差数列. …(4分)
的等差数列. …(4分)
可得数列 的通项公式
的通项公式 ,所
,所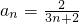 .…(6分)
.…(6分)
(Ⅱ)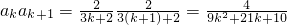 =
=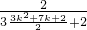 . …(8分)
. …(8分)
因为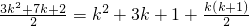 ,…(10分)
,…(10分)
k是正整数时, 一定是正整数,所以
一定是正整数,所以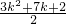 是正整数.
是正整数.
(也可以从k的奇偶性来分析)
所以ak•ak+1是数{an}中的项,是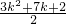 项. …(12分)
项. …(12分)
分析:(Ⅰ)通过对已知条件的转化,可以得到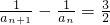 ,所以数列
,所以数列 是
是 为首项,公差
为首项,公差 的等差数列,继而可求an
的等差数列,继而可求an
(Ⅱ)得到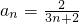 之后,ak•ak+1=
之后,ak•ak+1=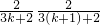 =
=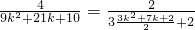 ,再去判断就容易了.
,再去判断就容易了.
点评:本题考查数列的递推关系,解题的关键是对条件合理转化,通过转化后可求an,从而可以判断ak•ak+1是否为数列an中的项.
∴
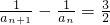 ,
,所以数列
 是
是 为首项,公差
为首项,公差 的等差数列. …(4分)
的等差数列. …(4分)可得数列
 的通项公式
的通项公式 ,所
,所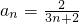 .…(6分)
.…(6分)(Ⅱ)
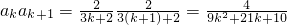 =
=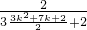 . …(8分)
. …(8分)因为
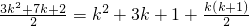 ,…(10分)
,…(10分)k是正整数时,
 一定是正整数,所以
一定是正整数,所以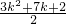 是正整数.
是正整数.(也可以从k的奇偶性来分析)
所以ak•ak+1是数{an}中的项,是
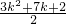 项. …(12分)
项. …(12分)分析:(Ⅰ)通过对已知条件的转化,可以得到
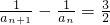 ,所以数列
,所以数列 是
是 为首项,公差
为首项,公差 的等差数列,继而可求an
的等差数列,继而可求an(Ⅱ)得到
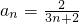 之后,ak•ak+1=
之后,ak•ak+1=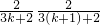 =
=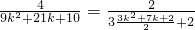 ,再去判断就容易了.
,再去判断就容易了.点评:本题考查数列的递推关系,解题的关键是对条件合理转化,通过转化后可求an,从而可以判断ak•ak+1是否为数列an中的项.

练习册系列答案
相关题目