题目内容
【题目】已知动圆![]() 的圆心为点
的圆心为点![]() ,圆
,圆![]() 过点
过点![]() 且与被直线
且与被直线![]() 截得弦长为
截得弦长为![]() .不过原点
.不过原点![]() 的直线
的直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点,且
两点,且![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)求三角形![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() .(2)16
.(2)16
【解析】
(1)设![]() ,根据圆的相交弦长公式,即可得出
,根据圆的相交弦长公式,即可得出![]() 关系;
关系;
(2)由(1)得,曲线![]() 方程为
方程为![]() ,根据已知可得
,根据已知可得![]() ,设直线方程为
,设直线方程为![]() ,与抛物线方程联立,得
,与抛物线方程联立,得![]() ,利用根与系数关系,将三角形
,利用根与系数关系,将三角形![]() 面积表示为
面积表示为![]() 的函数,根据函数特征,即可求出最小值.
的函数,根据函数特征,即可求出最小值.
(1)设![]() ,圆
,圆![]() 的半径
的半径![]()
圆![]() 到直线
到直线![]() 的距离
的距离![]()
由于圆![]() 被直线
被直线![]() 截得弦长为
截得弦长为![]() ,所以
,所以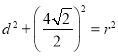
即 ,化简得,
,化简得,![]()
所以点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)由![]() 知
知![]() (或
(或![]() )
)
解法一:设![]() 直线
直线![]() 的方程为
的方程为![]()
由![]() 消去
消去![]() 得
得![]()
![]() 即
即![]()
![]() ,
,![]()
由![]() 即
即![]() ,即
,即![]()
由于![]() ,所以
,所以![]() ,
,
所以![]() 解得
解得![]()
所以直线![]() 方程为
方程为![]() 恒过定点
恒过定点![]()
三角形![]() 面积
面积
![]()
当![]() 时,
时,![]()
所以三角形![]() 面积的最小值为16.
面积的最小值为16.
解法二:设![]()
直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]()
由![]() ,解得
,解得 即
即![]() ,
,
所以![]()
同理可得![]()
三角形![]() 面积
面积
![]()
下面提供两种求最小值的思路:
思路1:利用基本不等式
![]() ,
,
当且仅当![]() 即
即![]() 时,
时,![]()
所以三角形![]() 面积的最小值为16.
面积的最小值为16.
思路2:用导数
不妨设![]() ,则
,则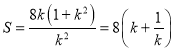 ,
,![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
所以当![]() 时,
时,
所以三角形![]() 面积的最小值为16.
面积的最小值为16.

练习册系列答案
相关题目