题目内容
在△ABC中,若
=
,则△ABC是( )
| cosA+2cosC |
| cosA+2cosB |
| b |
| c |
分析:根据正弦定理将已知条件中的等式变形,结合三角恒等变换化简得cosA[2sin(B-C)-(sinB-sinC)]=0,可得cosA=0或2sin(B-C)=sinB-sinC,再分情况讨论即可得到△ABC是等腰三角形或直角三角形.
解答:解:∵
=
,∴c(cosA+2cosC)=b(cosA+2cosB)
由正弦定理,得sinC(cosA+2cosC)=sinB(cosA+2cosB)
即cosA(sinB-sinC)=sin2C-sin2B=2cos(B+C)sin(C-B)
∵cos(B+C)=-cosA
∴cosA(sinB-sinC)=2cosAsin(B-C),移项得cosA[2sin(B-C)-(sinB-sinC)]=0
∴cosA=0或2sin(B-C)=sinB-sinC
①当cosA=0时,A=
,可得△ABC是直角三角形;
②若2sin(B-C)=sinB-sinC,
化简得sin
(2cos
-cos
)=0,
∵2cos
-cos
≠0,
∴sin
=0,可得B-C=0,得B=C,△ABC是等腰三角形
综上所述,△ABC是等腰三角形或直角三角形
故选:D
| cosA+2cosC |
| cosA+2cosB |
| b |
| c |
由正弦定理,得sinC(cosA+2cosC)=sinB(cosA+2cosB)
即cosA(sinB-sinC)=sin2C-sin2B=2cos(B+C)sin(C-B)
∵cos(B+C)=-cosA
∴cosA(sinB-sinC)=2cosAsin(B-C),移项得cosA[2sin(B-C)-(sinB-sinC)]=0
∴cosA=0或2sin(B-C)=sinB-sinC
①当cosA=0时,A=
| π |
| 2 |
②若2sin(B-C)=sinB-sinC,
化简得sin
| B-C |
| 2 |
| B-C |
| 2 |
| B+C |
| 2 |
∵2cos
| B-C |
| 2 |
| B+C |
| 2 |
∴sin
| B-C |
| 2 |
综上所述,△ABC是等腰三角形或直角三角形
故选:D
点评:本题给出三角形的边角关系式,判断三角形的形状,着重考查了正弦定理解三角形和三角恒等变换等知识,属于中档题.

练习册系列答案
相关题目
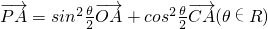 ,则
,则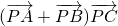 的最小值是________.
的最小值是________.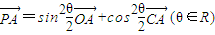 ,则
,则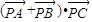 的最小值是 .
的最小值是 .