Question

已知点A（-1，0）、B（2，0），动点M满足2∠MAB=∠MBA,求点M的轨迹方程.

Answer 1

解析：设M（x,y）,∠MAB=α,则∠MBA=2α.

(1)当点M在x轴上方时，2α≠90°,y＞0,tanα=k_MA=,tan(π-2α)=.

又∵tan(π-2α)=-tan2α,

∴-.

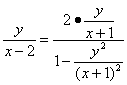化简得x²-=1.

∵|MA|＞|MB|,

∴x＞1.当2α=90°时，△MAB为等腰直角三角形，点（2，3）在曲线上.

(2)当点M在x轴下方时，同理可得点M的轨迹方程为x²-=1(x＞1,y＜0).

(3)当点M在线段AB上时，也满足2∠MAB=∠MBA，此时y=0(-1＜x＜2).

综上，点M的轨迹方程为x²-=1(x＞1)或y=0(-1＜x＜2).