题目内容
设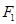 ,
,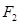 分别是椭圆
分别是椭圆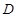 :
: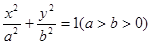 的左、右焦点,过
的左、右焦点,过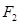 作倾斜角为
作倾斜角为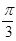 的直线交椭圆
的直线交椭圆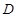 于
于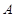 ,
,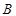 两点,
两点, 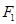 到直线
到直线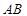 的距离为
的距离为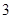 ,连结椭圆
,连结椭圆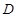 的四个顶点得到的菱形面积为
的四个顶点得到的菱形面积为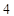 .
.
(1)求椭圆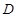 的方程;
的方程;
(2)过椭圆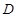 的左顶点
的左顶点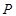 作直线
作直线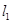 交椭圆
交椭圆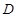 于另一点
于另一点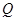 , 若点
, 若点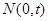 是线段
是线段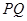 垂直平分线上的一点,且满足
垂直平分线上的一点,且满足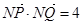 ,求实数
,求实数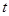 的值.
的值.
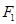 ,
,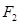 分别是椭圆
分别是椭圆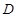 :
: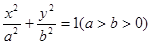 的左、右焦点,过
的左、右焦点,过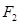 作倾斜角为
作倾斜角为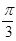 的直线交椭圆
的直线交椭圆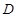 于
于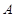 ,
,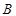 两点,
两点, 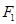 到直线
到直线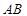 的距离为
的距离为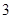 ,连结椭圆
,连结椭圆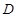 的四个顶点得到的菱形面积为
的四个顶点得到的菱形面积为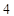 .
.(1)求椭圆
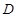 的方程;
的方程;(2)过椭圆
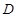 的左顶点
的左顶点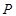 作直线
作直线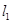 交椭圆
交椭圆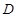 于另一点
于另一点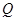 , 若点
, 若点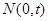 是线段
是线段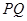 垂直平分线上的一点,且满足
垂直平分线上的一点,且满足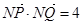 ,求实数
,求实数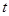 的值.
的值.(1)椭圆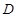 的方程为
的方程为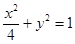 ;(2)满足条件的实数
;(2)满足条件的实数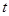 的值为
的值为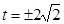 或
或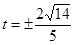 .
.
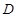 的方程为
的方程为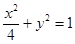 ;(2)满足条件的实数
;(2)满足条件的实数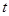 的值为
的值为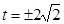 或
或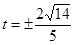 .
.试题分析:(1)利用椭圆的几何性质及
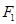 到直线
到直线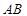 的距离为
的距离为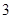 ,建立
,建立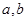 的方程组即得;
的方程组即得;(2)由(1)知:
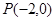 , 设
, 设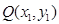
根据题意可知直线
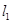 的斜率存在,可设直线斜率为
的斜率存在,可设直线斜率为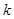 ,则直线
,则直线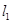 的方程为
的方程为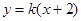
把它代入椭圆
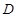 的方程,消去
的方程,消去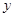 ,整理得:
,整理得: 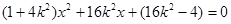
应用韦达定理以便于确定线段
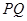 的中点坐标为
的中点坐标为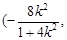
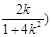 .
.讨论当
 ,
,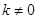 的情况,确定
的情况,确定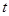 的值.
的值.试题解析:(1)设
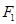 ,
,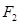 的坐标分别为
的坐标分别为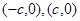 ,其中
,其中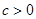
由题意得
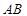 的方程为:
的方程为: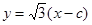
因
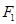 到直线
到直线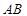 的距离为
的距离为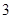 ,所以有
,所以有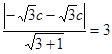 ,解得
,解得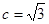 1分
1分所以有
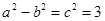 ①
①由题意知:
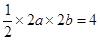 ,即
,即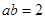 ②
②联立①②解得:
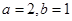
所求椭圆
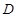 的方程为
的方程为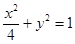 5分
5分(2)由(1)知:
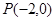 , 设
, 设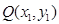
根据题意可知直线
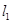 的斜率存在,可设直线斜率为
的斜率存在,可设直线斜率为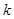 ,则直线
,则直线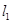 的方程为
的方程为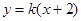
把它代入椭圆
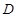 的方程,消去
的方程,消去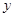 ,整理得:
,整理得: 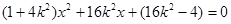
由韦达定理得
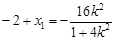 ,则
,则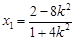 ,
,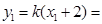
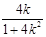 ,
,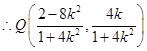 ,线段
,线段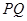 的中点坐标为
的中点坐标为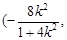
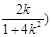 7分
7分(ⅰ)当
 时, 则有
时, 则有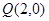 ,线段
,线段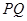 垂直平分线为
垂直平分线为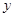 轴
轴于是
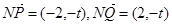
由
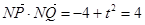 ,解得:
,解得: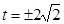 9分
9分(ii)因为点
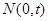 是线段
是线段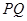 垂直平分线的一点,
垂直平分线的一点,令
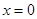 ,得:
,得: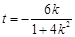 ,于是
,于是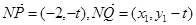
由
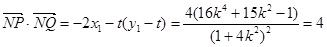 ,解得:
,解得: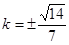
代入
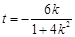 ,解得:
,解得: 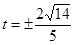
综上, 满足条件的实数
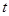 的值为
的值为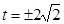 或
或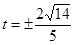 13分
13分
练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
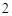 的椭圆
的椭圆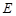 的两个顶点分别为
的两个顶点分别为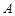 和
和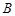 ,且
,且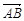 与n
与n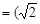 ,
,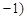 共线.
共线.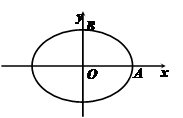
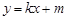 与椭圆
与椭圆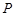 和
和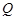 ,且原点
,且原点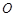 总在以
总在以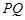 为直径的圆的内部,求实数
为直径的圆的内部,求实数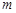 的取值范围.
的取值范围. ,
, 为小圆上的一条定直径,则以大圆的切线为准线,且过
为小圆上的一条定直径,则以大圆的切线为准线,且过 两点的抛物线焦点
两点的抛物线焦点 的轨迹方程为( )(以线段
的轨迹方程为( )(以线段 轴,其中垂线为
轴,其中垂线为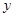 轴建立平面直角坐标系)
轴建立平面直角坐标系)



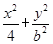 =1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为________.
=1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为________. =1(a>b>0)上任一点P到两个焦点的距离的和为2
=1(a>b>0)上任一点P到两个焦点的距离的和为2 ,P与椭圆长轴两顶点连线的斜率之积为-
,P与椭圆长轴两顶点连线的斜率之积为- .设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
.设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2). =
= (O为坐标原点),求|y1-y2|的值;
(O为坐标原点),求|y1-y2|的值; 上一点
上一点 到右焦点的距离是1,则点
到右焦点的距离是1,则点



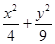 =1上任一点P,由点P向x轴作垂线PQ,垂足为Q,设点M在PQ上,且
=1上任一点P,由点P向x轴作垂线PQ,垂足为Q,设点M在PQ上,且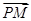 =2
=2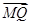 ,点M的轨迹为C.
,点M的轨迹为C.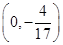 且平行于x轴的直线上一动点,且满足
且平行于x轴的直线上一动点,且满足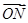 =
=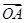 +
+ (O为原点),且四边形OANB为矩形,求直线l的方程.
(O为原点),且四边形OANB为矩形,求直线l的方程. 是椭圆上的一点,
是椭圆上的一点,  是焦点, 且, 则△
是焦点, 且, 则△ 的面积是
的面积是



 上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cosα=
上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cosα= ,sin(α+β)=
,sin(α+β)= ,则此椭圆的离心率为 .
,则此椭圆的离心率为 .