题目内容
如图，在直角坐标系中，中心在原点，焦点在x轴上的椭圆G的离心率为
，左顶点A（-4，0），圆O′：（x-2）2+y2=r2是椭圆G的内接△ABC的内切圆。
，左顶点A（-4，0），圆O′：（x-2）2+y2=r2是椭圆G的内接△ABC的内切圆。
（1）求椭圆G的方程；
（2）求圆O′的半径；
（3）过M（0，1）作圆O′的两条切线交椭圆于E，F，判断直线EF与圆的位置关系，并证明。
（2）求圆O′的半径；
（3）过M（0，1）作圆O′的两条切线交椭圆于E，F，判断直线EF与圆的位置关系，并证明。
解：（1）
，
得
椭圆方程为
；
（2）设B
，过圆心O′作
于D，
交长轴于H
由
得
即
①
又B
在椭圆上
②
由①、②式得
解得
或
（舍去）；
（3）直线EF与圆Ｏ′的相切
设过点
与圆
相切的直线方程为：
③
则
即
解得
将③代入
得
则异于零的解为
设
，
则
则直线EF的方程为
即
则圆心
到直线FE的距离
故结论成立。
，得椭圆方程为
；（2）设B
，过圆心O′作于D，交长轴于H由
得即
①又B
在椭圆上 ②由①、②式得
解得
或（舍去）；（3）直线EF与圆Ｏ′的相切
设过点
与圆相切的直线方程为： ③则
即
解得
将③代入
得则异于零的解为
设
，则
则直线EF的方程为
即
则圆心
到直线FE的距离故结论成立。
练习册系列答案
相关题目
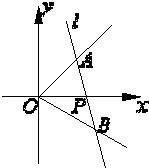如图，在直角坐标系中，射线OA：x-y=0（x≥0），OB：
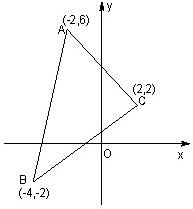如图，在直角坐标系中，已知△ABC的三个顶点的坐标，求：
如图，在直角坐标系中，直线y=6-x与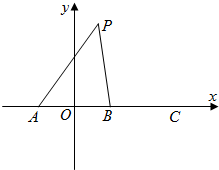
如图，在直角坐标系中，A，B，C三点在x轴上，原点O和点B分别是线段AB和AC的中点，已知AO=m（m为常数），平面上的点P满足PA+PB=6m．
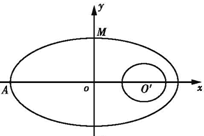如图，在直角坐标系中，中心在原点，焦点在x轴上的椭圆G的离心率为