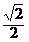题目内容
已知AB为半圆的直径,P为半圆上一点,以A、B为焦点且过点P做椭圆,当点P在半圆上移动时,椭圆的离心率有( )
分析:根据直径所对的圆周角为直角得到∠APB=90°,可得|PA|2+|PB|2=|AB|2,再利用基本不等式算出|PA|+|PB|≤
|AB|.再由以A、B为焦点的椭圆经过点P,利用椭圆的定义与离心率的公式加以计算,可得当|PA|=|PB|时,椭圆的离心率有最小值
.
| 2 |
| ||
| 2 |
解答:解: ∵AB为半圆的直径,点P在半圆上.
∵AB为半圆的直径,点P在半圆上.
∴∠APB=90°,可得|PA|2+|PB|2=|AB|2.
根据基本不等式,得(|PA|+|PB|)2≤2(|PA|2+|PB|2)=2|AB|2,
∴|PA|+|PB|≤
|AB|.
又∵以A、B为焦点的椭圆经过点P,
∴椭圆的长轴2a=|PA|+|PB|,焦距2c=|AB|,
由此可得椭圆的离心率e=
=
≥
=
.
即当|PA|=|PB|时,椭圆的离心率有最小值
.
故选:D
 ∵AB为半圆的直径,点P在半圆上.
∵AB为半圆的直径,点P在半圆上.∴∠APB=90°,可得|PA|2+|PB|2=|AB|2.
根据基本不等式,得(|PA|+|PB|)2≤2(|PA|2+|PB|2)=2|AB|2,
∴|PA|+|PB|≤
| 2 |
又∵以A、B为焦点的椭圆经过点P,
∴椭圆的长轴2a=|PA|+|PB|,焦距2c=|AB|,
由此可得椭圆的离心率e=
| 2c |
| 2a |
| |AB| |
| |PA|+|PB| |
| |AB| | ||
|
| ||
| 2 |
即当|PA|=|PB|时,椭圆的离心率有最小值
| ||
| 2 |
故选:D
点评:本题给出以半圆的直径AB为焦点的椭圆经过半圆上一点P,求椭圆离心率的最值.着重考查了圆周角定理、利用基本不等式求最值和椭圆的简单几何性质等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•辽宁模拟)选修4-1:几何证明选讲
(2012•辽宁模拟)选修4-1:几何证明选讲 (2011•太原模拟)如图,已知AB为半圆O的直径,BE、CD分别为半圆的切线,切点分别为B、C,DC的延长线交BE于F,AC的延长线交BE于E.AD⊥DC,D为垂足.
(2011•太原模拟)如图,已知AB为半圆O的直径,BE、CD分别为半圆的切线,切点分别为B、C,DC的延长线交BE于F,AC的延长线交BE于E.AD⊥DC,D为垂足. B.最小值
B.最小值 D.最小值
D.最小值