题目内容
（本小题满分14分）
在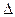
ABC中角A,B,C的对边分别为a,b,c,且满足（2a-c）cosB=bcosC
(1)求角B的大小；
(2设向量m= (sinA,cos2A),n=(k,1)，且m
n＞1恒成立，求k的取值范围.
（1）∵(2a－c)cosB=bcosC，∴（2sinA－sinC）cosB=sinBcosC.
即2sinAcosB=sinBcosC+sinCcosB=sin(B+C)
∵A+B+C=π，∴2sinAcosB="sinA " 3分
∵0<A<π,∴sinA>0.∴cosB=
∵0<B<π，B= 
5分
（2）
=ksinA+cos2A=－2sin2A+ksinA+1，A∈（0，
） 7分
设sinA=t，则t∈
，则=－2t2+kt+1＞1
10分
由t∈∴2t最大值为2，所以 k>2 14分
解析
练习册系列答案
天天向上一本好卷系列答案
相关题目
，
，B=45°求A、C及c 
中，
为边
上的一点，
，
，
，求
．
,b,c分别是三个内角A,B,C所对边，若
，
,
,求△ABC的面积S.
中，内角A，B，C的对边分别是
求a，b.
最大值．某巡逻艇在A处发现在北偏东
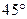距A处8处有一走私船，正沿东偏南
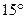的方向以12海里/小时的速度向我岸行驶，巡逻艇立即以
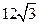海里/小时的速度沿直线追击，问巡逻艇最少需要多长时间才能追到走私船，并指出巡逻艇航行方向。
且
－
＝（2
－
）bc，sinA·sinB＝
，BC边上中线AM的长为
．